A lower bound on the radius of a graph

Description of the problem

Assume we have an undirected graph \(G\) given as a pair of sets \((V,E)\) where \(V\) is a finite set of vertices and \(E\subset\binom{V}{2}\) is a collection of subsets of \(V\) each of size 2 denoting the set of edges.

The distance between two vertices is the length of the shortest path between these vertices. Eccentricity of a vertex is defined to be the largest distance from that vertex.

\[ Ecc(x)=max_{y\in V} d(x,y) \]

Now, we can define the radius and diameter of a graph as

\[ Rad(G)=min_{x\in V} Ecc(x) \quad\text{ and }\quad\ Diam(G)=max_{x\in V} Ecc(x) \]

Today, I would like to find a lower bound on the radius of \(G\) by calculating two cheaper quantities: the number of vertices and the largest degree in the graph. Let us recall that the degree of a vertex is the number of edges connected to that vertex.

Eccentricity

Here is an algorithm that I used earlier to calculate the eccentricity of a vertex \(x\):

Function Eccentricity
Input: A vertex x and a graph G
Output: Eccentricity of x in G
Begin
  Initialize R = 0
  Initialize W = {x}
  Initialize V = Vertices of G \ {x}
  While V is non-empty
    Let W = the intersection of V and the set of 
            vertices adjacent to a vertex in W
    Let V = V \ W
    Increase R
  End while
  Return R
End

which I re-implemented in common lisp as follows:

(defun eccentricity (x G)
   (labels ((vicinity (u)
               (delete u
                  (remove-duplicates
                     (vertices
                        (remove-if-not (lambda (e) (member u e)) G))))))
      (let* ((A (vertices G))
             (size (length A)))
         (do ((n 0 (1+ n))
              (V (delete x A) (set-difference V W))
              (W (vicinity x)
                 (intersection V (mapcan #'vicinity W))))
             ((or (null V) (> n size)) n)))))`</pre>

VERTICES
ECCENTRICITY

For this implementation, a graph is represented as a list of edges where and edge is a list that contains two vertices. Using this implementation, now I can define the radius as:

(defun radius (G)
  (reduce #'min (mapcar (lambda (v) (eccentricity v G)) (vertices G))))

RADIUS

Let me test this on the following tree

(defvar tree '((-3 -1) (-4 -1) (-5 -2) (-6 -2) (-1 0) (-2 0) (0 1) 
               (1 2) (1 3) (2 4) (2 5) (3 6) (3 7) (4 8) (4 9) (5 10) 
               (5 11) (6 12) (6 13) (7 14) (7 15)))

TREE

(mapcar (lambda (v) (eccentricity v tree)) (vertices tree))
(radius tree)

(6 6 6 6 5 5 4 3 4 4 6 5 6 6 5 6 6 5 6 6 5 6)
3

A lower bound on the radius

In the first step of the eccentricity algorithm, we delete one vertex. Assume we have \[ k = \max_{v\in V} deg(v) \] Then in the second step we delete less than or equal to \(k\) vertices. But at each next step, the number of edges we deleted is multiplied at most by \(k-1\). Thus we obtain \[ \|V\| \leq 1 + k + k(k-1) + \cdots k(k-1)^{Ecc(v)-1} = 1 + \sum_{i=0}^{Ecc(v)-1} k(k-1)^i \] Let us distinguish two cases: \(k=2\) and \(k\>2\). In the first case we get \[ \|V\| \leq 1 + k\cdot Ecc(v) \] which means \[ Ecc(v) \geq \frac{\|V\|-1}{k} \] In the second case we have \[ \|V\| \leq 1 + \frac{k\left((k-1)^{Ecc(v)}-1\right)}{k-2} \] Playing with the equation, we get \[ Ecc(v)\geq \frac{\log\left((\|V\|-1)\left(1-\frac{2}{k}\right)+1\right)}{\log(k-1)} \] The inequality holds for every vertex \(v\). Thus we get 

\[ \min_{v\in V}Ecc(v) = Rad(G)\geq \begin{cases} \frac{\|V\|-1}{k} & \text{ if } k=2\\ \frac{\log\left((\|V\|-1)\left(1-\frac{2}{k}\right)+1\right)}{\log(k-1)} & \text{ if } k\>2 \end{cases} \]

Let us look at some examples. First, our approximation function:

(defun approx (G)
   (labels ((degree (x) (length (remove-if-not (lambda (e) (member x e :test #'equal)) G))))
       (let* ((vertices (remove-duplicates (reduce #'append G)))
              (k (reduce #'max (mapcar #'degree vertices)))
              (n (length vertices)))
          (cond ((< k 2) nil)
                ((= k 2) (ceiling (/ (- n 1.0) 2)))
                (t (ceiling (/ (log (+ 1.0d0 (* (1- n) (/ (- k 2) k))))
                               (log (- k 1.0d0)))))))))

APPROX

Let us see first for \(K_5\):

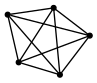
(radius K5)
(approx K5)

1
1

The inequality is indeed an equality. For the binary tree we used earlier

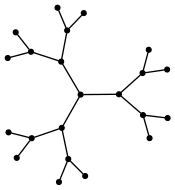
we get

(radius tree)
(approx tree)

3
3

So, the inequality is tight in this direction too. For graphs of type \(A_n\) and \(C_n\), we have \(k=2\).

(radius A7)
(approx A7)

4
4

In other words, the inequality is still the best we can hope for for these graphs too.

Ok. Now, for a random graph:

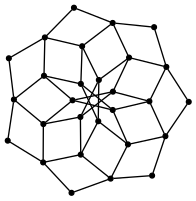
(radius graph)
(approx graph)

4
3

An analysis

For highly connected graphs, the lower bound is going to be worse since we would be badly overestimating the number of vertices we deleted in each step of the algorithm. For example for the following graph we get

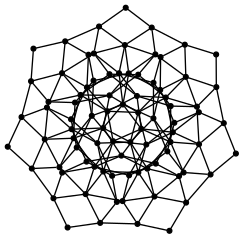
(radius graph1)
(approx graph1)

6
3

The complete graphs \(K_n\) are exempt from the overestimation since our algorithm terminates at step 1 already.