Eccentricity, Radius and Diameter in a Graph, Revisited

A previous post on this blog on radius and diameter of a graph gets a lot of traffic consistently. I have been looking at the code and one can refactor it to make it more efficient.

Edge-list Representation vs Topological Representation

In almost all of my posts on graphs on this blog, I have been usingthe set of edges as a representation for a graph. Today, I am going to represent graphs topologically, that is, by listing the neighboring vertices of a given vertex. For example, the graph whose edge list representation is

(defvar G '((0 1) (1 2) (1 3) (2 4) (3 4) (0 4)))
G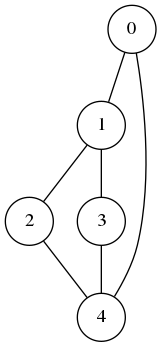

can also be represented by

((0 1 4) (1 0 2 3) (2 1 4) (3 1 4) (4 0 2 3))

where each sublist is a cons pair where the car is the vertex and cdr is the list of vertices adjacent to that vertex.

I am going to need a function that makes the conversion:

(defun convert (G)
  (let ((H (remove-duplicates
            (union G (mapcar #'reverse G))
            :test #'equal))
        (res nil))
    (dolist (edge H res)
      (if (assoc (car edge) res)
          (push (cadr edge) (cdr (assoc (car edge) res)))
          (push (copy-list edge) res)))))
CONVERT

(defvar H (convert G))

((4 0 3 2) (1 0 2 3) (2 1 4) (3 1 4) (0 1 4))

Since lists are ordered and I want an undirected graph, you see in the code that I take the union of edges and reverse edges.

Now, a utility function that returns the list of vertices of a given graph.

(defun vertices (G)
   (remove-duplicates (reduce #'append G)))
VERTICES

The beauty of this function lies in the fact that it returns the correct set for both representations:

(vertices G)
(1 2 3 0 4)

(vertices H)
(2 3 0 1 4)

And now the eccentricity function:

(defun eccentricity (x G)
  (let* ((A (vertices G))
         (size (length A)))
    (labels ((vicinity (u) (assoc u G)))
      (do ((n 0 (1+ n))
           (V A (set-difference V W))
           (W (vicinity x)
              (intersection V (reduce #'append (mapcar #'vicinity W)))))
          ((or (null V) (> n size)) n)))))
ECCENTRICITY

This function comes with a warning: the return value is not correct for disconnected graphs. The eccentricity of a graph can not be greater than the number of edges. So, if you see this function returning number of vertices plus 1, understand that the graph was disconnected.

(eccentricity 0 H)
2

Once we have that, the radius and the diameter function is defined the same way:

(defun radius-and-diameter (G)
   (let* ((H (convert G))
          (base (mapcar (lambda (x) (eccentricity x H)) (vertices H))))
      (list (apply #'min base) (apply #'max base))))
RADIUS-AND-DIAMETER

and we get

(radius-and-diameter G)
(2 2)

And if you recall, the distance function is very similar to the eccentricity function:

(defun dist (x y G)
  (let* ((A (vertices G))
         (size (length A)))
    (labels ((vicinity (u) (assoc u G)))
      (do ((n 1 (1+ n))
           (V A (set-difference V W))
           (W (vicinity x)
              (intersection V (reduce #'append (mapcar #'vicinity W)))))
          ((or (member y W) (> n size)) n)))))
DIST

and we get

(loop for i from 0 below 4 append
   (loop for j from (1+ i) to 4 collect
       (list i j (dist i j H))))
((0 1 1) (0 2 2) (0 3 2) (0 4 1) (1 2 1) (1 3 1) (1 4 2) (2 3 2) (2 4 1)
 (3 4 1))