Non-crossing Partitions and Dyck Words

Description of the problem

Working with Dyck words and non-crossing linear chords, I realized that one can also generate all non-crossing partitions of a finite set using Dyck words. I just need a new conversion function.

Non-crossing partitions

Consider the finite set \(\[n\] = {0,1,\ldots,n}\) and a partition \(\mathcal{P}\) of \(n\). We call such a partition as non-crossing if the corresponding chord diagram has no crossings.

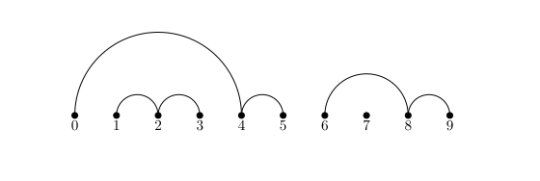
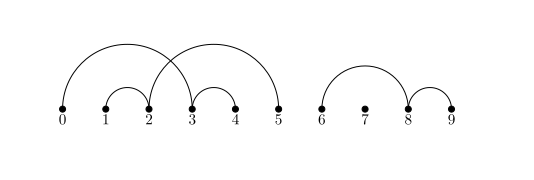
Implementation

Let me start with a slightly improved version of the generation of all Dyck words of a specific length:

(defun dyck-words (n &optional (a 0) (acc '(())))
  (labels ((insert (xxs ys)
             (mapcar (lambda (xs) (append xs ys)) xxs)))
    (if (= a n)
        (insert acc (loop repeat n collect 1))
        (append (dyck-words n (1+ a) (insert acc '(0)))
                (if (> a 0) (dyck-words (1- n) (1- a) (insert acc '(1))))))))

Next, a new function that converts a Dyck word into a non-crossing partition:

(defun unwind (xs stack &optional res)
  (if (or (null xs) (= 0 (car xs)))
      (values xs stack res)
      (unwind (cdr xs) (cdr stack) (cons (car stack) res))))

(defun convert (xs &optional (pos 0) stack res)
  (cond ((null xs) res)
        ((= 0 (car xs)) (convert (cdr xs) (1+ pos) (cons pos stack) res))
        (t (multiple-value-bind
                (ys st re) (unwind xs stack)
              (convert ys pos st (cons re res))))))

(mapcar #'convert (dyck-words 6))

(((0 1 2 3 4 5)) ((0 1 2 3 5) (4)) ((0 1 2 5) (3 4)) ((0 1 5) (2 3 4))
 ((0 5) (1 2 3 4)) ((5) (0 1 2 3 4)) ((0 1 2 4 5) (3)) ((0 1 2 5) (4) (3))
 ((0 1 5) (2 4) (3)) ((0 5) (1 2 4) (3)) ((5) (0 1 2 4) (3)) ((0 1 4 5) (2 3))
 ((0 1 5) (4) (2 3)) ((0 5) (1 4) (2 3)) ((5) (0 1 4) (2 3)) ((0 4 5) (1 2 3))
 ((0 5) (4) (1 2 3)) ((5) (0 4) (1 2 3)) ((4 5) (0 1 2 3)) ((5) (4) (0 1 2 3))
 ((0 1 3 4 5) (2)) ((0 1 3 5) (4) (2)) ((0 1 5) (3 4) (2)) ((0 5) (1 3 4) (2))
 ((5) (0 1 3 4) (2)) ((0 1 4 5) (3) (2)) ((0 1 5) (4) (3) (2))
 ((0 5) (1 4) (3) (2)) ((5) (0 1 4) (3) (2)) ((0 4 5) (1 3) (2))
 ((0 5) (4) (1 3) (2)) ((5) (0 4) (1 3) (2)) ((4 5) (0 1 3) (2))
 ((5) (4) (0 1 3) (2)) ((0 3 4 5) (1 2)) ((0 3 5) (4) (1 2))
 ((0 5) (3 4) (1 2)) ((5) (0 3 4) (1 2)) ((0 4 5) (3) (1 2))
 ((0 5) (4) (3) (1 2)) ((5) (0 4) (3) (1 2)) ((4 5) (0 3) (1 2))
 ((5) (4) (0 3) (1 2)) ((3 4 5) (0 1 2)) ((3 5) (4) (0 1 2))
 ((5) (3 4) (0 1 2)) ((4 5) (3) (0 1 2)) ((5) (4) (3) (0 1 2))
 ((0 2 3 4 5) (1)) ((0 2 3 5) (4) (1)) ((0 2 5) (3 4) (1)) ((0 5) (2 3 4) (1))
 ((5) (0 2 3 4) (1)) ((0 2 4 5) (3) (1)) ((0 2 5) (4) (3) (1))
 ((0 5) (2 4) (3) (1)) ((5) (0 2 4) (3) (1)) ((0 4 5) (2 3) (1))
 ((0 5) (4) (2 3) (1)) ((5) (0 4) (2 3) (1)) ((4 5) (0 2 3) (1))
 ((5) (4) (0 2 3) (1)) ((0 3 4 5) (2) (1)) ((0 3 5) (4) (2) (1))
 ((0 5) (3 4) (2) (1)) ((5) (0 3 4) (2) (1)) ((0 4 5) (3) (2) (1))
 ((0 5) (4) (3) (2) (1)) ((5) (0 4) (3) (2) (1)) ((4 5) (0 3) (2) (1))
 ((5) (4) (0 3) (2) (1)) ((3 4 5) (0 2) (1)) ((3 5) (4) (0 2) (1))
 ((5) (3 4) (0 2) (1)) ((4 5) (3) (0 2) (1)) ((5) (4) (3) (0 2) (1))
 ((2 3 4 5) (0 1)) ((2 3 5) (4) (0 1)) ((2 5) (3 4) (0 1)) ((5) (2 3 4) (0 1))
 ((2 4 5) (3) (0 1)) ((2 5) (4) (3) (0 1)) ((5) (2 4) (3) (0 1))
 ((4 5) (2 3) (0 1)) ((5) (4) (2 3) (0 1)) ((3 4 5) (2) (0 1))
 ((3 5) (4) (2) (0 1)) ((5) (3 4) (2) (0 1)) ((4 5) (3) (2) (0 1))
 ((5) (4) (3) (2) (0 1)) ((1 2 3 4 5) (0)) ((1 2 3 5) (4) (0))
 ((1 2 5) (3 4) (0)) ((1 5) (2 3 4) (0)) ((5) (1 2 3 4) (0))
 ((1 2 4 5) (3) (0)) ((1 2 5) (4) (3) (0)) ((1 5) (2 4) (3) (0))
 ((5) (1 2 4) (3) (0)) ((1 4 5) (2 3) (0)) ((1 5) (4) (2 3) (0))
 ((5) (1 4) (2 3) (0)) ((4 5) (1 2 3) (0)) ((5) (4) (1 2 3) (0))
 ((1 3 4 5) (2) (0)) ((1 3 5) (4) (2) (0)) ((1 5) (3 4) (2) (0))
 ((5) (1 3 4) (2) (0)) ((1 4 5) (3) (2) (0)) ((1 5) (4) (3) (2) (0))
 ((5) (1 4) (3) (2) (0)) ((4 5) (1 3) (2) (0)) ((5) (4) (1 3) (2) (0))
 ((3 4 5) (1 2) (0)) ((3 5) (4) (1 2) (0)) ((5) (3 4) (1 2) (0))
 ((4 5) (3) (1 2) (0)) ((5) (4) (3) (1 2) (0)) ((2 3 4 5) (1) (0))
 ((2 3 5) (4) (1) (0)) ((2 5) (3 4) (1) (0)) ((5) (2 3 4) (1) (0))
 ((2 4 5) (3) (1) (0)) ((2 5) (4) (3) (1) (0)) ((5) (2 4) (3) (1) (0))
 ((4 5) (2 3) (1) (0)) ((5) (4) (2 3) (1) (0)) ((3 4 5) (2) (1) (0))
 ((3 5) (4) (2) (1) (0)) ((5) (3 4) (2) (1) (0)) ((4 5) (3) (2) (1) (0))
 ((5) (4) (3) (2) (1) (0)))