Non-crossing Linear Chords
If you haven’t heard: Southeast of Turkey is hit (twice in a day) earthquakes of magnitude 7.4 and 7.8 this week. The government response has been inept, slow, and inadequate in most places. The reasons for this are long-coming. There is a huge relief effort by volunteers, national and international relief organizations. I urge you to donate to an international organization of your choosing, or a national (AHBAP, AFAD, AKUT) relief organization.
Description of the problem
I needed something that would occupy my mind and prevent me from reading news 24/7. So, I chose this.
For a natural number \(n\geq 1\), consider the set \(\[2n\]={0,1,\ldots,2n}\). A partition \(\mathcal{P}\) of \(\[2n\]\) is called a linear chord of length \(n\) if for every \(X\in \mathcal{P}\) we have \(\|X\|=2\). We usually represent these chords with chord diagrams such as
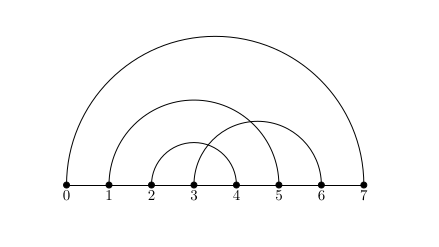
A linear chord is called non-crossing if a chord diagram with non-overlapping chords can be drawn.
Notice that the set of all non-crossing linear chords of length \(n\) is the same as the set of balanced brackets of length \(2n\). Using this fact, today I am going to write a common lisp program that lists all non-crossing linear chords.
A First Implementation
I am not going to explain the code below. It is a heavily modified version I took from Geeks for Geeks.
(defun ncc (n &optional result xs stack (position 0) (begin 0) (end 0))
(if (= n end)
(cons xs result)
(let ()
(if (> begin end)
(setf result (ncc n
result
(cons (list (car stack) position) xs)
(cdr stack)
(1+ position)
begin
(1+ end))))
(if (< begin n)
(setf result (ncc n
result
xs
(cons position stack)
(1+ position)
(1+ begin)
end)))
result)))
NNCHere are some examples:
(format nil "~{~a~%~%~}~%" (loop for i from 1 to 5 collect (nnc i)))
(((0 1)))
(((0 3) (1 2)) ((2 3) (0 1)))
(((0 5) (1 4) (2 3)) ((0 5) (3 4) (1 2)) ((4 5) (0 3) (1 2))
((2 5) (3 4) (0 1)) ((4 5) (2 3) (0 1)))
(((0 7) (1 6) (2 5) (3 4)) ((0 7) (1 6) (4 5) (2 3)) ((0 7) (5 6) (1 4) (2 3))
((6 7) (0 5) (1 4) (2 3)) ((0 7) (3 6) (4 5) (1 2)) ((0 7) (5 6) (3 4) (1 2))
((6 7) (0 5) (3 4) (1 2)) ((4 7) (5 6) (0 3) (1 2)) ((6 7) (4 5) (0 3) (1 2))
((2 7) (3 6) (4 5) (0 1)) ((2 7) (5 6) (3 4) (0 1)) ((6 7) (2 5) (3 4) (0 1))
((4 7) (5 6) (2 3) (0 1)) ((6 7) (4 5) (2 3) (0 1)))
(((0 9) (1 8) (2 7) (3 6) (4 5)) ((0 9) (1 8) (2 7) (5 6) (3 4))
((0 9) (1 8) (6 7) (2 5) (3 4)) ((0 9) (7 8) (1 6) (2 5) (3 4))
((8 9) (0 7) (1 6) (2 5) (3 4)) ((0 9) (1 8) (4 7) (5 6) (2 3))
((0 9) (1 8) (6 7) (4 5) (2 3)) ((0 9) (7 8) (1 6) (4 5) (2 3))
((8 9) (0 7) (1 6) (4 5) (2 3)) ((0 9) (5 8) (6 7) (1 4) (2 3))
((0 9) (7 8) (5 6) (1 4) (2 3)) ((8 9) (0 7) (5 6) (1 4) (2 3))
((6 9) (7 8) (0 5) (1 4) (2 3)) ((8 9) (6 7) (0 5) (1 4) (2 3))
((0 9) (3 8) (4 7) (5 6) (1 2)) ((0 9) (3 8) (6 7) (4 5) (1 2))
((0 9) (7 8) (3 6) (4 5) (1 2)) ((8 9) (0 7) (3 6) (4 5) (1 2))
((0 9) (5 8) (6 7) (3 4) (1 2)) ((0 9) (7 8) (5 6) (3 4) (1 2))
((8 9) (0 7) (5 6) (3 4) (1 2)) ((6 9) (7 8) (0 5) (3 4) (1 2))
((8 9) (6 7) (0 5) (3 4) (1 2)) ((4 9) (5 8) (6 7) (0 3) (1 2))
((4 9) (7 8) (5 6) (0 3) (1 2)) ((8 9) (4 7) (5 6) (0 3) (1 2))
((6 9) (7 8) (4 5) (0 3) (1 2)) ((8 9) (6 7) (4 5) (0 3) (1 2))
((2 9) (3 8) (4 7) (5 6) (0 1)) ((2 9) (3 8) (6 7) (4 5) (0 1))
((2 9) (7 8) (3 6) (4 5) (0 1)) ((8 9) (2 7) (3 6) (4 5) (0 1))
((2 9) (5 8) (6 7) (3 4) (0 1)) ((2 9) (7 8) (5 6) (3 4) (0 1))
((8 9) (2 7) (5 6) (3 4) (0 1)) ((6 9) (7 8) (2 5) (3 4) (0 1))
((8 9) (6 7) (2 5) (3 4) (0 1)) ((4 9) (5 8) (6 7) (2 3) (0 1))
((4 9) (7 8) (5 6) (2 3) (0 1)) ((8 9) (4 7) (5 6) (2 3) (0 1))
((6 9) (7 8) (4 5) (2 3) (0 1)) ((8 9) (6 7) (4 5) (2 3) (0 1)))A Second Implementation
As I was finishing the implementation above, I remembered that the set of balanced brackets of length \(n\) is bijective to the set of Dyck Words, and I already implemented a lisp function that returns the set of all Dyck words of a given length. I just need a function that converts a Dyck word into a non-overlapping linear chord.
(defun dyck-words (n &optional (a 0) (acc '(())))
(labels ((insert (i xs &optional (m 1))
(let ((y (loop repeat m collect i)))
(mapcar (lambda (x) (append y x)) xs))))
(if (= a n)
(insert 0 acc n)
(append (dyck-words n (1+ a) (insert 1 acc))
(if (> a 0) (dyck-words (1- n) (1- a) (insert 0 acc)))))))
(dyck-words 4)
DYCK-WORDS
((0 0 0 0 1 1 1 1) (0 1 0 0 0 1 1 1) (0 0 1 0 0 1 1 1) (0 0 0 1 0 1 1 1)
(0 0 0 1 1 0 1 1) (0 0 1 0 1 0 1 1) (0 1 0 0 1 0 1 1) (0 0 1 1 0 0 1 1)
(0 1 0 1 0 0 1 1) (0 0 0 1 1 1 0 1) (0 0 1 0 1 1 0 1) (0 1 0 0 1 1 0 1)
(0 0 1 1 0 1 0 1) (0 1 0 1 0 1 0 1))Here is the conversion function:
(defun convert (xs &optional stack res (pos 0))
(cond
((null xs) (nreverse res))
((= 0 (car xs)) (convert (cdr xs) (cons pos stack) res (1+ pos)))
(t (convert (cdr xs) (cdr stack) (cons (list (car stack) pos) res) (1+ pos)))))
CONVERTHere are the same set of examples above:
(format nil "~{~a~%~%~}~%" (loop for i from 1 to 5 collect (mapcar #'convert (dyck-words i))))
(((0 1)))
(((1 2) (0 3)) ((0 1) (2 3)))
(((2 3) (1 4) (0 5)) ((1 2) (3 4) (0 5)) ((0 1) (3 4) (2 5))
((1 2) (0 3) (4 5)) ((0 1) (2 3) (4 5)))
(((3 4) (2 5) (1 6) (0 7)) ((0 1) (4 5) (3 6) (2 7)) ((1 2) (4 5) (3 6) (0 7))
((2 3) (4 5) (1 6) (0 7)) ((2 3) (1 4) (5 6) (0 7)) ((1 2) (3 4) (5 6) (0 7))
((0 1) (3 4) (5 6) (2 7)) ((1 2) (0 3) (5 6) (4 7)) ((0 1) (2 3) (5 6) (4 7))
((2 3) (1 4) (0 5) (6 7)) ((1 2) (3 4) (0 5) (6 7)) ((0 1) (3 4) (2 5) (6 7))
((1 2) (0 3) (4 5) (6 7)) ((0 1) (2 3) (4 5) (6 7)))
(((0 1) (2 3) (4 5) (7 8) (6 9)) ((1 2) (0 3) (4 5) (7 8) (6 9))
((0 1) (3 4) (2 5) (7 8) (6 9)) ((1 2) (3 4) (0 5) (7 8) (6 9))
((2 3) (1 4) (0 5) (7 8) (6 9)) ((0 1) (2 3) (5 6) (7 8) (4 9))
((1 2) (0 3) (5 6) (7 8) (4 9)) ((0 1) (3 4) (5 6) (7 8) (2 9))
((1 2) (3 4) (5 6) (7 8) (0 9)) ((2 3) (1 4) (5 6) (7 8) (0 9))
((2 3) (4 5) (1 6) (7 8) (0 9)) ((1 2) (4 5) (3 6) (7 8) (0 9))
((0 1) (4 5) (3 6) (7 8) (2 9)) ((3 4) (2 5) (1 6) (7 8) (0 9))
((3 4) (2 5) (6 7) (1 8) (0 9)) ((0 1) (4 5) (6 7) (3 8) (2 9))
((1 2) (4 5) (6 7) (3 8) (0 9)) ((2 3) (4 5) (6 7) (1 8) (0 9))
((2 3) (1 4) (6 7) (5 8) (0 9)) ((1 2) (3 4) (6 7) (5 8) (0 9))
((0 1) (3 4) (6 7) (5 8) (2 9)) ((1 2) (0 3) (6 7) (5 8) (4 9))
((0 1) (2 3) (6 7) (5 8) (4 9)) ((3 4) (5 6) (2 7) (1 8) (0 9))
((0 1) (5 6) (4 7) (3 8) (2 9)) ((1 2) (5 6) (4 7) (3 8) (0 9))
((2 3) (5 6) (4 7) (1 8) (0 9)) ((4 5) (3 6) (2 7) (1 8) (0 9))
((3 4) (2 5) (1 6) (0 7) (8 9)) ((0 1) (4 5) (3 6) (2 7) (8 9))
((1 2) (4 5) (3 6) (0 7) (8 9)) ((2 3) (4 5) (1 6) (0 7) (8 9))
((2 3) (1 4) (5 6) (0 7) (8 9)) ((1 2) (3 4) (5 6) (0 7) (8 9))
((0 1) (3 4) (5 6) (2 7) (8 9)) ((1 2) (0 3) (5 6) (4 7) (8 9))
((0 1) (2 3) (5 6) (4 7) (8 9)) ((2 3) (1 4) (0 5) (6 7) (8 9))
((1 2) (3 4) (0 5) (6 7) (8 9)) ((0 1) (3 4) (2 5) (6 7) (8 9))
((1 2) (0 3) (4 5) (6 7) (8 9)) ((0 1) (2 3) (4 5) (6 7) (8 9)))