Bron-Kerbosch Algorithm in Clojure

Description of the problem

Assume we have a simple undirected graph \(G=(V,E)\). Then a subset \(C\) of the set of vertices \(V\) is called a clique if for every pair of distinct elements \(a,b\in C\) the pair \(\{a,b\}\) is an edge in \(G\). The set of all cliques of a graph is partially ordered under set inclusion. A clique is called maximal if it is a maximal element in this poset. Today, I am going to implement a version of the Bron-Kerbosch Algorithm which finds the set of all maximal cliques in a graph. I wrote about it earlier but that version was in common lisp, and today I am going to write an implementation from scratch in clojure.

An implementation in clojure

Let us start with a clean namespace with the necessary libraries loaded:

(ns bron-kerbosch
  (:use clojure.set))

I am going to represent a graph as a set of edges where each edge is a pair of distinct elements chosen from the underlying set of vertices. I am going to need two utility functions for later. The first returns the set of vertices for a given graph, while the second returns the set of neighbors of a given vertex in a given graph.

(defn vertices [graph] (reduce union graph))

(defn neighbors [v graph]
  (difference (reduce union (filter #(contains? % v) graph))
             #{v}))

#'bron-kerbosch/vertices
#'bron-kerbosch/neighbors

Finally, the main function, which is implemented as a recursive function:

(defn bron-kerbosch 
    ([graph] (bron-kerbosch graph (vertices graph) #{} #{} #{}))
    ([graph p x r res]
     (if (and (empty? x) (empty? p)) 
         (union #{r} res)
         (loop [ps p
                xs x
                cs res]
             (if (empty? ps)
                 cs
                 (let [v (first ps)
                       nv (neighbors v graph)]
                    (recur (into #{} (rest ps))
                           (union #{v} xs)
                           (bron-kerbosch graph
                                          (intersection ps nv)
                                          (intersection xs nv)
                                          (union #{v} r)
                                          cs))))))))

#'bron-kerbosch/bron-kerbosch

In order to test the code, I am going to need a function that generates a random simple graph:

(defn get-random-graph [n m k]
  (->> (range n)
       (mapcat (fn [i] (repeatedly m (fn [] #{i (+ 1 i (rand-int k))}))))
       distinct
       (into #{})))

#'bron-kerbosch/get-random-graph

OK. Here is a random graph:

(def random-graph (get-random-graph 12 5 9))
random-graph

#'bron-kerbosch/random-graph
#{#{13 5} #{19 11} #{3 11} #{6 3} #{0 1} #{14 10} #{15 11} #{13 9} #{7 16} #{7 6} #{2 10} #{3 5} #{5 10} #{12 10} #{0 4} #{3 10} #{3 12} #{11 16} #{17 11} #{0 7} #{4 8} #{0 3} #{5 14} #{7 13} #{10 8} #{6 11} #{6 8} #{17 10} #{12 5} #{4 10} #{7 2} #{13 11} #{15 8} #{1 6} #{9 10} #{4 2} #{7 9} #{1 3} #{15 9} #{1 10} #{4 9} #{1 9} #{13 10} #{14 8} #{17 8} #{0 5} #{10 18}}

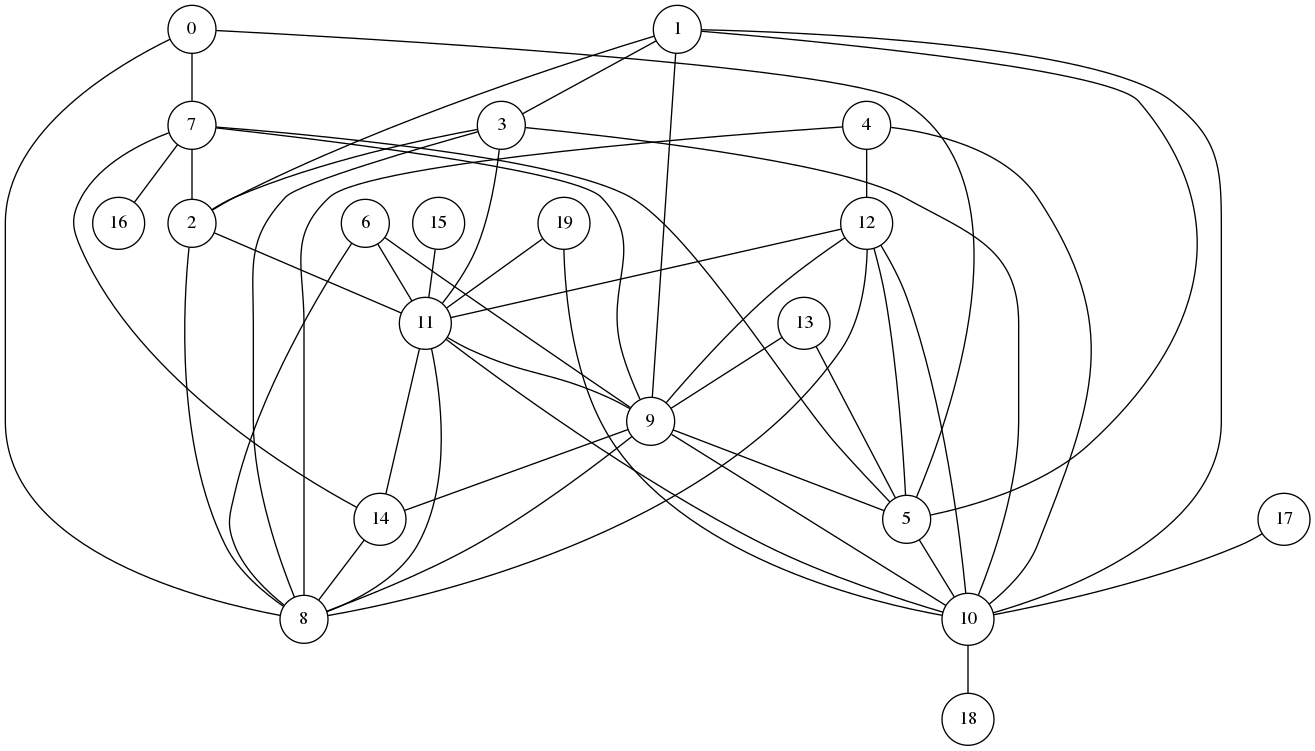
And now, let us test our main function on this random graph:

(bron-kerbosch random-graph)

#{#{3 12 5 10} #{19 11} #{15 11} #{7 16} #{7 6} #{0 4} #{11 16} #{17 11} #{0 7} #{14 10 8} #{5 14 10} #{7 13 9} #{1 6 3} #{1 9 10} #{6 8} #{7 2} #{13 9 10} #{1 3 10} #{13 11} #{15 8} #{0 1 3} #{0 3 5} #{6 3 11} #{15 9} #{17 10 8} #{4 9 10} #{4 10 8} #{4 2 10} #{13 5 10} #{10 18}}