Listing all Young Tableaux

Description of the problem:

A \(k\) partition of \(n\) is a sequence of numbers \(1\leq n_1\leq \cdots\leq n_k\) such that \(n = \sum_i n_i\). We usually visualize such partitions as blocks stacked on top of each other as follows:

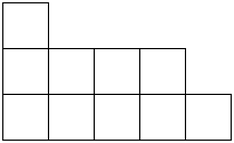
You can read the diagram above as the partition \(1\leq 4\leq 5\), or its conjugate as \(3\geq 2\geq 2\geq 2\geq 1\). I have written about conjugate partitions before.

A Young tableau is a partition filled with numbers 1 through n such that all numbers in a row or a column are ordered from smallest to the largest. For example the diagram

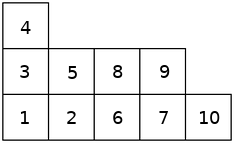
belongs to a Young tableau but this next one

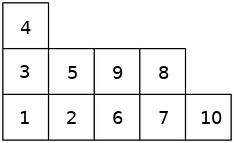
does not come from a valid Young tableau.

Today, I am going to write a scala program that lists all possible Young tableaux of a given size. The algorithm is simple: for Young tableaux of size \(n+1\) take all Young tableaux of size \(n\) and insert \(n+1\) in every possible position satisfying the constraints that the resulting diagram is still a Young tableau.

Implementation

If you followed this blog long enough, you probably know that I like common lisp a lot. But this is one of those problems in which one can rreally leverage a good type system and a rich set of data structures. Scala is a good tool for that.

The following function recursively inserts an integer into a Young tableau returning a set of all possible insertions:

def youngInsert(m:Int, ys:List[List[Int]], xs:List[List[Int]] = List[List[Int]]()): Set[List[List[Int]]] = {
    def helper(bs:List[List[Int]], as:List[List[Int]]):List[List[Int]] = {
        if(bs.isEmpty) 
            as:+List(m)
        else if(bs.head.head < m && (as.isEmpty || as.last.length > bs.head.length)) 
            as ++ List(bs.head:+m) ++ bs.tail
        else 
            helper(bs.tail, as:+bs.head)
    }
    if(ys.isEmpty) 
        Set(xs:+List(m))
    else 
        youngInsert(m, ys.tail, xs:+ys.head) + helper(ys,xs)
}`

And the following function iterates the procedure until we reach the desired number:

def youngTableaux(n:Int, m:Int=2, acc:Set[List[List[Int]]] = Set(List(List(1)))):Set[List[List[Int]]] = {    
    if(m>n)
      acc.toSet
    else
      youngTableaux(n,m+1,acc.flatMap(x=>youngInsert(m,x))).toSet
}

Let us test:

(1 to 10).map(x=>youngTableaux(x).size)
res0: scala.collection.immutable.IndexedSeq[Int] = Vector(1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496)

These are the first 10 terms in Sloane’s A000085 which are the number of standard Young tableaux of size 1 through 10.

Now, let us see a list of all possible Young tableaux:

youngTableaux(4).foreach(println)
List(List(1, 3), List(2, 4))
List(List(1, 3, 4), List(2))
List(List(1, 4), List(2), List(3))
List(List(1, 2, 4), List(3))
List(List(1), List(2), List(3), List(4))
List(List(1, 2, 3), List(4))
List(List(1, 2), List(3), List(4))
List(List(1, 3), List(2), List(4))
List(List(1, 2), List(3, 4))
List(List(1, 2, 3, 4))

A lisp implementation

I couldn’t help myself, and wrote a common lisp implementation:

(defun insert (m ys &optional xs)
  (labels ((helper (bs as)
             (cond ((null bs) (append as (list (list m))))
                   ((and (< (caar bs) m)
                         (or (null as)
                             (> (length (car (reverse as)))
                                (length (car bs)))))
                    (append as
                            (list (append (car bs) (list m)))
                            (cdr bs)))
                   (t (helper (cdr bs) (append as (list (car bs))))))))
    (if (null ys)
        (list (append xs (list (list m))))
        (remove-duplicates
           (append (insert m (cdr ys) (append xs (list (car ys))))
                   (list (helper ys xs)))
           :test #'equal))))

(defun young-tableaux (n &optional (m 2) (acc (list (list (list 1)))))
  (if (> m n)
      (remove-duplicates acc :test #'equal)
      (young-tableaux n (1+ m) (mapcan (lambda (x) (insert m x)) acc))))

INSERT
YOUNG-TABLEAUX

Let us test this too:

(format t "~{~a~%~}" (young-tableaux 4))

((1) (2) (3) (4))
((1 4) (2) (3))
((1 3) (2) (4))
((1 3) (2 4))
((1 3 4) (2))
((1 2) (3) (4))
((1 2) (3 4))
((1 2 4) (3))
((1 2 3) (4))
((1 2 3 4))

NIL