Collatz sequence (yet again)
Description of the problem:
I will consider the following function
\[ f(1) = 1, \quad f(n) = f(n/2) \text{ if $n$ is even },\quad f(n) = 3n+1 \text{ otherwise } \]
and the recursive sequence \[ a_{n+1} = f(a_n) \] with an arbitrary initial value \(a_0\).
Famous Collatz conjecture states that this sequence always stabilizes with tail being an infinite sequence of 1’s.
Today, I am interested in the expected value of the 2-part of the sequence until it terminates at 1. In particular, I would like to calculate \[ E(a_0) = \frac{1}{\ell(a_0)} \sum_n \nu_2(a_n) \] where \[ \nu_2(n) = \max\{m\in\mathbb{N}\mid 2^m \text{ divides } n\} \] and \(\ell(a_0)\) is the length of the Collatz sequence starting at \(a_0\).
Implementation
Let us write our functions
(defun f(n)
(cond ((= n 1) 1)
((evenp n) (f (/ n 2)))
(t (1+ (* 3 n)))))
(defun nu2(n &optional (acc 0))
(if (oddp n)
acc
(nu2 (/ n 2) (1+ acc))))
(defun collatz (a0 &optional acc)
(if (= a0 1)
(nreverse acc)
(collatz (f a0) (cons a0 acc))))
(defun expected (a0)
(let ((xs (collatz a0)))
(/ (reduce #'+ (mapcar #'nu2 xs))
(length xs)
1.0)))
F
NU2
COLLATZ
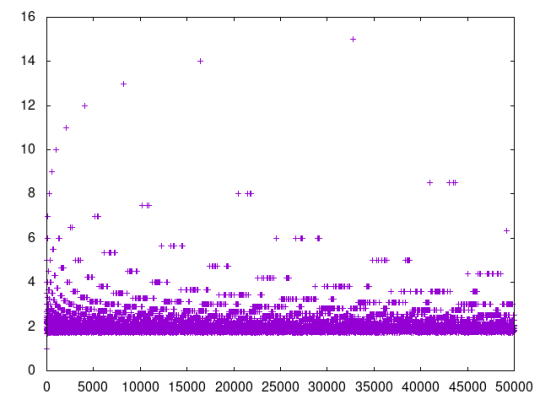
EXPECTEDLet us see the plot of the expected values between 2 and 50000:
(with-open-file (out "collatz-2part-data.csv"
:direction :output
:if-exists :supersede
:if-does-not-exist :create)
(loop for i from 2 to 50000 do
(format out "~4d, ~4,3f~%" i (expected i))))
NIL