Expected Value of the Diameter of a Tree
Description of the problem
Gil Kalai asks the following problem: given a random tree on \(n\) vertices, what is the expected value of its diameter?
According to Kalai, the expected value of the diameter of a random
tree on \(n\) vertices asymptotically
behaves like \(\sqrt{n}\).
We can certainly devise an experiment to see that this is the case.
Random trees and diameter
I have talked about uniformly generating random trees and measuring diameters of graphs before: here, here and here. So, let us put them to use for this problem. As before, I will use a list of two vertices to denote an edge, and a list of such edges to denote a graph.
First, I need a function to generate uniformly random trees
(defun random-tree (n)
(loop for i from 1 below n
collect (list (random i) i)))
RANDOM-TREEand three other functions to measure the diameter
(defun vertices (G)
(remove-duplicates (reduce #'union G)))
(defun eccentricity (x G)
(let* ((A (vertices G))
(size (length A))
(nbhd (let ((H (remove-duplicates
(union G (mapcar #'reverse G))
:test #'equal))
(res nil))
(dolist (edge H res)
(if (assoc (car edge) res)
(push (cadr edge) (cdr (assoc (car edge) res)))
(push (copy-list edge) res))))))
(labels ((vicinity (u) (assoc u nbhd)))
(do ((n 0 (1+ n))
(V A (set-difference V W))
(W (vicinity x)
(intersection V (reduce #'append (mapcar #'vicinity W)))))
((or (null V) (> n size)) n)))))
(defun diameter-radius (G)
(let ((bag (loop for v in (vertices G) collect (eccentricity v G))))
(cons (reduce #'max bag) (reduce #'min bag))))
VERTICES
ECCENTRICITY
DIAMETER-RADIUSHere is a function to measure the expected value of diameter of a random tree on \(n\) vertices by generating \(n^{3/2}\) such graphs and measuring the average diameter.
(defun test (n)
(let* ((m (floor (expt n 1.5)))
(bag (loop repeat m collect (diameter-radius (random-tree n)))))
(cons (/ (reduce #'+ (mapcar #'car bag)) m)
(/ (reduce #'+ (mapcar #'cdr bag)) m))))
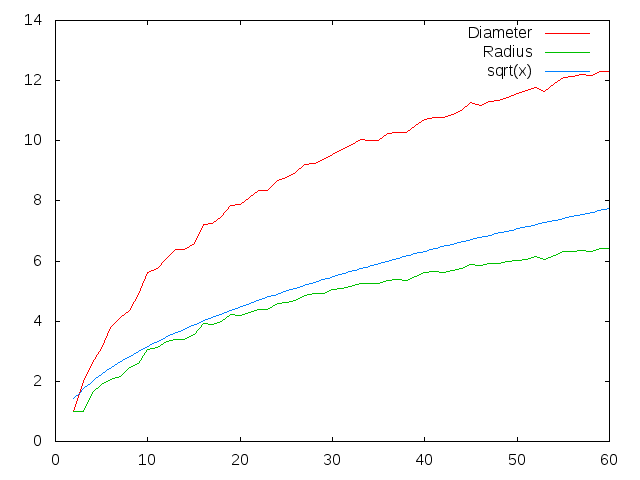
TESTHere is a graph of the results for \(n=2\) to \(n=60\).