Transitive Closure of a Directed Graph or a Relation

Description of the problem

Assume we have a set $X$ and a relation $R:X\to X$ on $X$. One can think of $R$ as a directed graph on vertices labelled by elements of $X$. I have written about transitive closure before, but the code I wrote then was in python. Today, we are doing lisp(s).

Let us recall: The transitive closure of $R$ is a new directed graph (or a new relation) such that if two vertices $x$ and $y$ are connected by an oriented path, then $x$ and $y$ are connected via an edge.

An algorithm

Today’s implementation is based on the following algorithm:

For each vertex $x$ do steps 2 and 3 below.
Find the longest paths starting at $x$.
For each path in this collection and for each vertex $y$ in this path add $(x,y)$ as a new edge.

An Implementation in Common Lisp

Here is my implementation of a function that returns all of longest paths in a graph. As usual, I represent graphs as list of pairs of vertices.

(defun longest-paths (edges)
  (labels ((process (path)
             (let* ((end (car path))
                    (pool (remove-if-not (lambda (x) (equal (car x) end)) edges)))
               (if (null pool)
                   (list path)
                   (mapcar (lambda (edge) (cons (cadr edge) path)) pool))))
           (helper (paths)
             (let ((temp (mapcan #'process paths)))
               (if (equal temp paths)
                   (mapcar #'reverse paths)
                   (helper temp)))))
     (mapcan (lambda (edge) (helper (list (reverse edge)))) edges)))

LONGEST-PATHS

Let me test:

(defvar graph '((0 1) (1 2) (1 3) (2 4) (5 6) (6 7)))
(longest-paths graph)

GRAPH
((0 1 2 4) (0 1 3) (1 2 4) (1 3) (2 4) (5 6 7) (6 7))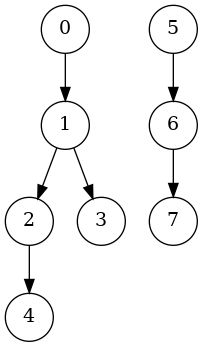

And here is the closure function:

(defun closure (edges)
  (remove-duplicates 
     (mapcan (lambda (path)
                (if (equal 2 (length path))
                    (list path)
                    (let ((y (car path))
                          (xs (cdr path)))
                       (mapcar (lambda (x) (list y x)) xs))))
             (longest-paths edges))
     :test #'equal))

CLOSURE

And let us test again:

(closure graph)

((0 2) (0 4) (0 1) (0 3) (1 2) (1 4) (1 3) (2 4) (5 6) (5 7) (6 7))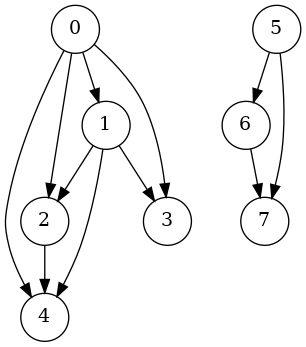

An Implementation in Clojure

Here is another implementation done in clojure:

(defn closure [edges]
  (letfn [(helper [xs]
            (let [temp (filter (fn [[u v]] (= (last xs) u)) edges)]
              (if (empty? temp)
                #{xs}
                (map (fn [[u v]] (concat xs [v])) temp))))
          (finish [xs]
            (if (= 2 (count xs))
              #{xs}
              (into #{} (map (fn [y] [(first xs) y]) (rest xs)))))]
    (loop [prev edges]
      (let [next (into #{} (mapcat helper prev))]
        (if (= prev next)
          (into #{} (mapcat finish prev))
          (recur next))))))