Some Hasse Diagrams
Today is nice pictures day :) I’ll be giving you pictures of Hasse
diagrams of few posets of shuffles. First, a function for
shuffles:
(defun shuffles (xs ys &optional (acc (list nil)))
(labels ((insert (a as)
(mapcar (lambda (x) (cons a x)) as))
(paste (as bs)
(mapcar (lambda (b) (append (reverse b) as)) bs)))
(cond ((null xs) (paste ys acc))
((null ys) (paste xs acc))
(t (append (shuffles (cdr xs) ys (insert (car xs) acc))
(shuffles xs (cdr ys) (insert (car ys) acc)))))))
SHUFFLESI’ll check the adjacency by being different by a transposition or a cyclic transposition:
(defun connected-by-a-transpose-p (xs ys)
(let* ((zs (mapcar (lambda (x y) (if (equal x y) 0 1)) xs ys)))
(and (= 2 (reduce #'+ zs))
(every #'equal '(1 1) (member 1 zs)))))
(defun connected-by-a-cyclic-rotation-p (xs ys)
(labels ((cyclep (as bs)
(equal as (append (cdr bs) (list (car bs))))))
(or (cyclep xs ys) (cyclep ys xs))))
(defun adjacentp (xs ys)
(or (connected-by-a-transpose-p xs ys)
(connected-by-a-cyclic-rotation-p xs ys)))
CONNECTED-BY-A-TRANSPOSE-P
CONNECTED-BY-A-CYCLIC-ROTATION-P
ADJACENTPNext, a function for generating the graph for the Hasse diagram and next a function writing the graphviz dot file:
(defun hasse (xs pred)
(mapcon (lambda (ys)
(let ((y (car ys))
(zs (cdr ys))
(res nil))
(dolist (z zs res)
(if (and (not (member (list y z) res :test #'equal))
(not (member (list z y) res :test #'equal))
(funcall pred z y))
(push (list z y) res)))))
xs))
(defun write-dot (G filename &optional (engine "neato") (shape "point"))
(progn
(with-open-file (dot-file (format nil "~A.dot" filename)
:direction :output
:if-exists :supersede
:if-does-not-exist :create)
(format dot-file "graph G {~% node[shape=~A]; ~% ~{ ~{\"~{~A~}\" -- \"~{~A~}\"; ~} ~% ~} }~%" shape G))
(uiop:run-program
(format nil "~A -T png -o ~A.png ~:*~A.dot" engine filename))
(format nil "~%" filename)))
HASSE
WRITE-DOTI am going to need two helper function:
(defun rep (n k &optional acc)
(if (= n 0)
acc
(rep (1- n) k (cons k acc))))
(defun range (a b &optional (k 1) acc)
(if (= a b)
(nreverse acc)
(range (+ a k) b k (cons a acc))))
REP
RANGEOK. Here are the graphs:
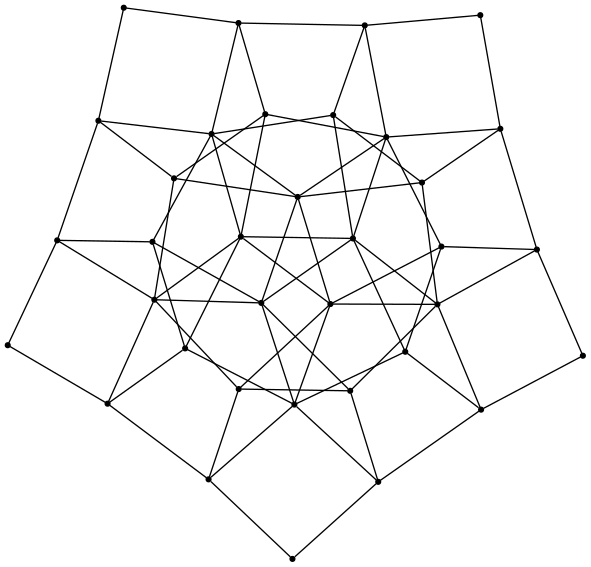
(defvar graph1 (hasse (shuffles (range 0 2) (rep 4 3)) #'adjacentp))
GRAPH1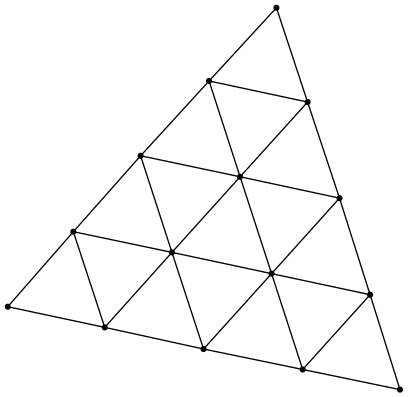
Next one:
(defvar graph2 (hasse (shuffles (range 0 6) (rep 2 "*")) #'adjacentp))
GRAPH2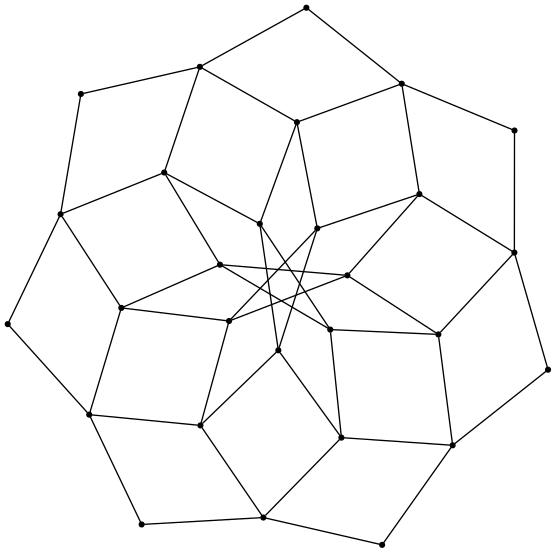
Finally,
(defvar graph3 (hasse (shuffles (range 0 4) (rep 3 "*")) #'adjacentp))
GRAPH3