Lattice of Dyck Words
Description of the problems
I will call an arbitrary sequence of 0’s and 1’s balanced if the number of 0’s and 1’s are the same. I will call a balanced sequence positive if in every initial segment of the sequence, the number of 0’s is greater than or equal to the number of 1’s. For example,
(0 1 0 1 0 0 1 1)is a positive balanced sequence, while
(1 0 0 1) is not.
The proper name for a positive balanced sequence is a Dyck word. Today, I am going to write a short common lisp function that returns all Dyck words of a certain length.
An implementation
This following is the first implementation I came up with:
(defun dyck-words (n &optional (a 0) (b n) (acc (list nil)))
(labels ((insert (i xs) (mapcar (lambda (x) (cons i x)) xs)))
(cond ((= a n) (mapcar (lambda (x) (append (loop repeat b collect 0) x)) acc))
((= a 0) (dyck-words n (1+ a) b (insert 1 acc)))
(t (union (dyck-words n (1+ a) b (insert 1 acc))
(dyck-words (1- n) (1- a) (1- b) (insert 0 acc)))))))
DYCK-WORDSHere the index \(n\) refers to the number of 0′s and 1′s. One can refactor it to be a little shorter:
(defun dyck-words (n &optional (a 0) (b n) (acc (list nil)))
(labels ((insert (i xs) (mapcar (lambda (x) (cons i x)) xs)))
(if (= a n)
(mapcar (lambda (x) (append (loop repeat b collect 0) x)) acc)
(union (dyck-words n (1+ a) b (insert 1 acc))
(if (> a 0) (dyck-words (1- n) (1- a) (1- b) (insert 0 acc)))))))
DYCK-WORDSI prefer the first one even though it is longer. I think it is more readable.
Here is a test. The set of Dyck words of length 8:
(dyck-words 4)
((0 0 0 1 1 1 0 1) (0 0 1 0 1 1 0 1) (0 1 0 0 1 1 0 1) (0 1 0 1 0 1 0 1)
(0 0 1 1 0 1 0 1) (0 0 1 1 0 0 1 1) (0 1 0 1 0 0 1 1) (0 1 0 0 1 0 1 1)
(0 0 1 0 1 0 1 1) (0 0 0 1 1 0 1 1) (0 0 0 1 0 1 1 1) (0 0 1 0 0 1 1 1)
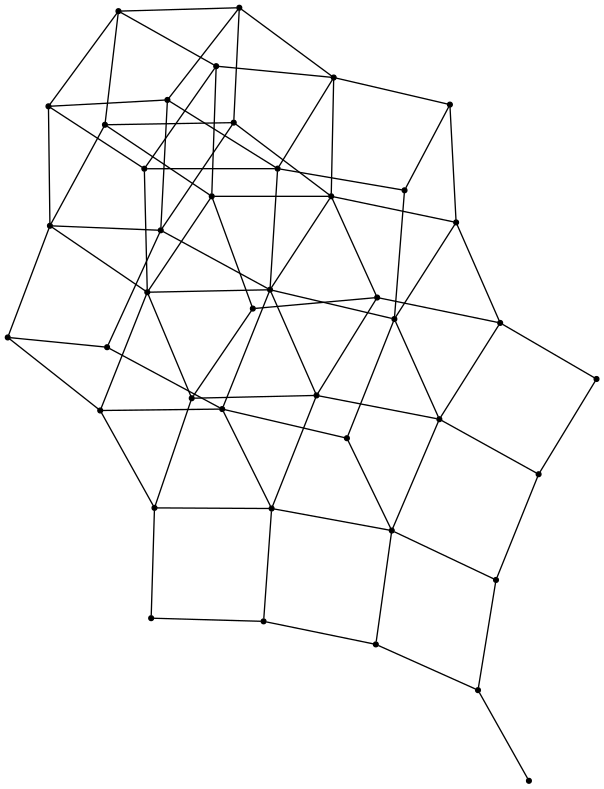
(0 1 0 0 0 1 1 1) (0 0 0 0 1 1 1 1))Lattice of Dyck words
I am going to create a graph out of Dyck words of a certain length. Two Dycks words are going to be connected if one is obtained from the other using a single transposition, i.e. by switching two consecutive letters. The following function checks if two Dyck words are connected by a single transposition.
(defun adjacentp (xs ys)
(labels ((vec-xor (x y)
(mapcar (lambda (x y) (if (equal x y) 0 1)) x y)))
(let ((res (vec-xor xs ys)))
(and (= 2 (reduce #'+ res))
(every #'equal '(1 1) (member 1 res))))))
ADJACENTPHere is the code for the graph:
(defun hasse (xs pred)
(mapcon (lambda (ys)
(let ((y (car ys))
(zs (cdr ys))
(res nil))
(dolist (z zs res)
(if (funcall pred y z)
(push (list y z) res)))))
xs))
HASSELet us see the graph for the set of Dyck words of length 8:
(defvar dyck8 (hasse (dyck-words 4) #'adjacentp))
DYCK8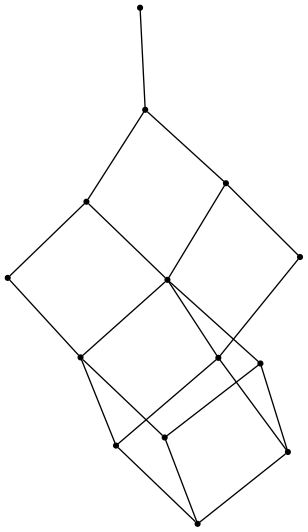
Now, Dyck words of length 10:
(defvar dyck10 (hasse (dyck-words 5) #'adjacentp))
DYCK10