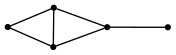
The poset of connected subgraphs of a connected graph
Today I will give you some nice pictures. But first, let me give you the basic setup.
Posets, total orders and Hasse diagrams
A poset is a set with what is called a partial order. This order relation allows us to compare elements. A total order is a partial order where any two elements can be compared. Think of natural numbers and the less than or equal to relation. Not every partial order is a total order though. For example, the subset relation on a collection of sets need not be total.
We can represent posets with their Hasse diagrams. I have written about Hasse diagrams before. Here is the reverse Hasse diagram for the set of subsets of \(\{0,1\}\).
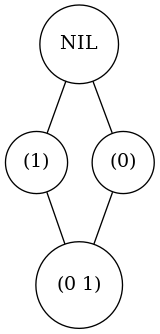
I call it “reverse” because nil had to be at the bottom.
I am using graphviz and most of
the time I don’t care what the graph layout should be. I am not going to
start now.
As you can see in this example that our poset \(\{\emptyset,\{0\},\{1\},\{0,1\}\}\) together with the subset relation is not totally ordered since \(\{0\}\) and \(\{1\}\) can not be compared.
A chain is a totally ordered subset of a poset. For example, \(\{\emptyset,\{0\},\{0,1\}\}\) is a chain in the previous example.
Graphs
Now, consider a connected graph \(G=(V,E)\) where \(V\) is the set of vertices and \(E\) is the set of edges between vertices. Today, I am going to consider simple graphs. This means if two vertices are connected by an edge, then they are connected with a single edge only.
If we take a subset \(W\subset V\) of vertices there is an induced subgraph of \(G\) on these vertices. I will call a subset connected if the induced subgraph is connected.
Now, our graph \(G\) comes with a poset: the poset of connected subgraphs of \(G\). Today, I going to draw you the Hasse diagram of the poset of connected subgraphs of some standard graphs.
The poset of connected subgraphs
For the code today, I am going to need a functions that checks equality of sets
(defun set-equal-p (xs ys)
(and (subsetp xs ys) (subsetp ys xs)))
SET-EQUAL-PNext, I will write three functions that give three classes of graphs: the line graph on \(n\) vertices, the cycle graph on \(n\) vertices and the complete graph on \(n\)-vertices:
(defun a (n)
(loop for i from 0 below (1- n) collect
(list i (1+ i))))
(defun c (n)
(loop for i from 0 below n collect
(list i (mod (1+ i) n))))
(defun k (n)
(loop for i from 0 below (1- n) append
(loop for j from (1+ i) to (1- n) collect (list i j))))
A
C
KOur next piece is
(defun extend (xs G)
(mapcar (lambda (x) (union xs (list x)))
(set-difference
(reduce #'union
(remove-if-not
(lambda (e) (some (lambda (v) (member v e)) xs))
G))
xs)))
EXTENDFor a given graph (as list of edges) and a collection of vertices,
the function extend finds the list of vertices that are
connected to a vertex in xs in \(G\), and then gives the list of all
connected subsets extending xs. Let us test it on an
example. So, consider the cycle graph on 4 vertices:
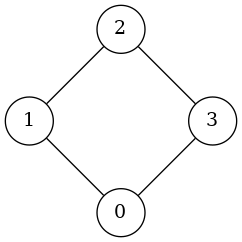
Let us find the connected subsets extending already connected subset \({0,3}\)
(extend '(0 3) (c 4))
((3 0 1) (3 0 2))Now, the following function gives us a collection of subsets of \(V\) whose induced subgraphs are connected in \(G\).
(defun poset (G)
(let ((vs (reduce #'union G)))
(remove-duplicates
(mapcan (lambda (x)
(do* ((xss (list (list x)) yss)
(yss (mapcan (lambda (xs) (extend xs G)) xss)
(mapcan (lambda (xs) (extend xs G)) xss))
(zss (union xss yss) (union zss yss)))
((null yss) zss)))
vs)
:test #'set-equal)))
POSETLet us test it on the cycle graph on 4 vertices:
(poset (c 4))
((2) (1 2) (1) (2 3 1) (3 2) (3) (1 0 3 2) (1 0 2) (3 0 2) (3 0 1) (0 1) (0 3)
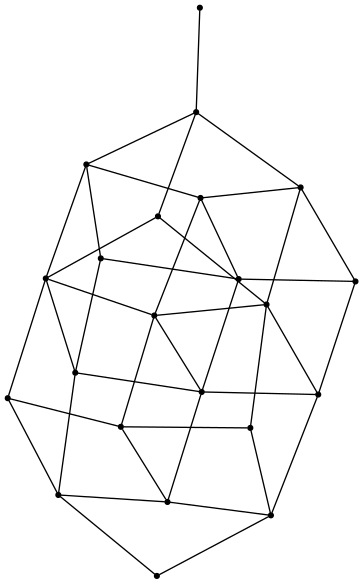
(0))The following is definitely not the Hasse diagram, but it is a nice visualization. Vertices are connected subsets. I put an edge between two such subsets only if one extends the other with a single element.
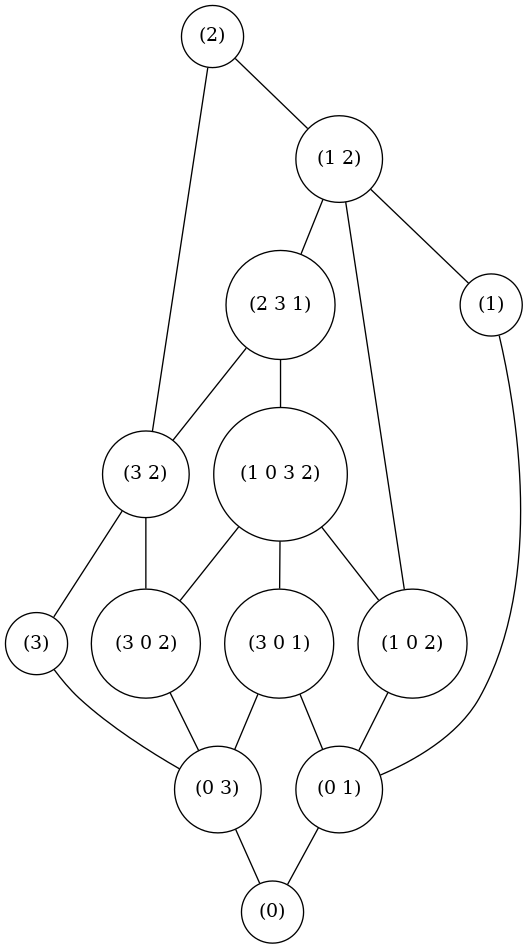
Here are the code for the Hasse graph of the poset and the drawing routine:
(defun write-dot (G filename &optional (engine "neato") (shape "point"))
(progn
(with-open-file (dot-file (format nil "~A.dot" filename)
:direction :output
:if-exists :supersede
:if-does-not-exist :create)
(format dot-file "graph G {~% node[shape=~A]; ~% ~{ ~{\"~A\" -- \"~A\"; ~} ~% ~} }~%" shape G))
(uiop:run-program
(format nil "~A -T png -o ~A.png ~:*~A.dot" engine filename))
(format nil "~%" filename)))
(defun hasse (xs &optional acc)
(if (null (cdr xs))
acc
(let ((x (car xs))
(zs (cdr xs))
(ys acc))
(hasse (cdr xs)
(dolist (z zs ys)
(if (= 1 (+ (length (set-difference z x))
(length (set-difference x z))))
(push (list x z) ys)))))))
WRITE-DOT
HASSELet us do few others. In order to simplify the pictures, I will not put labels on the vertices:
The graph for the poset of connected subgraphs of the complete graph
on 4 vertices:
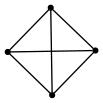
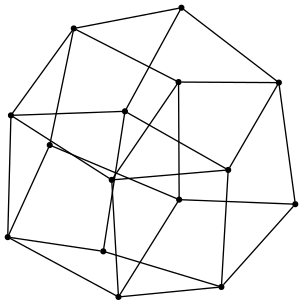
The graph for the poset of connected subgraphs of the line graph on 5
vertices

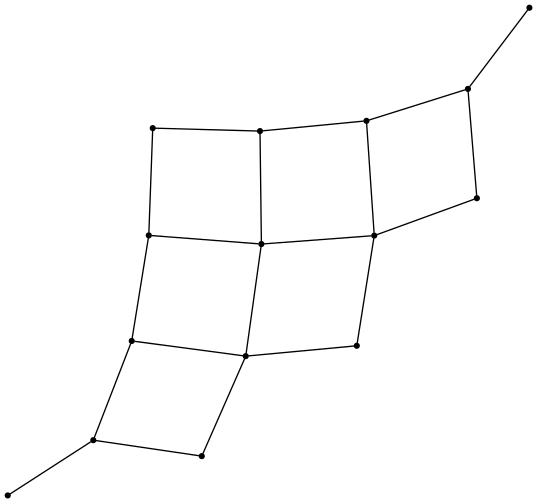
The graph for the poset of connected subgraphs of the cycle graph on 8 vertices
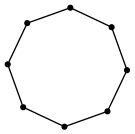
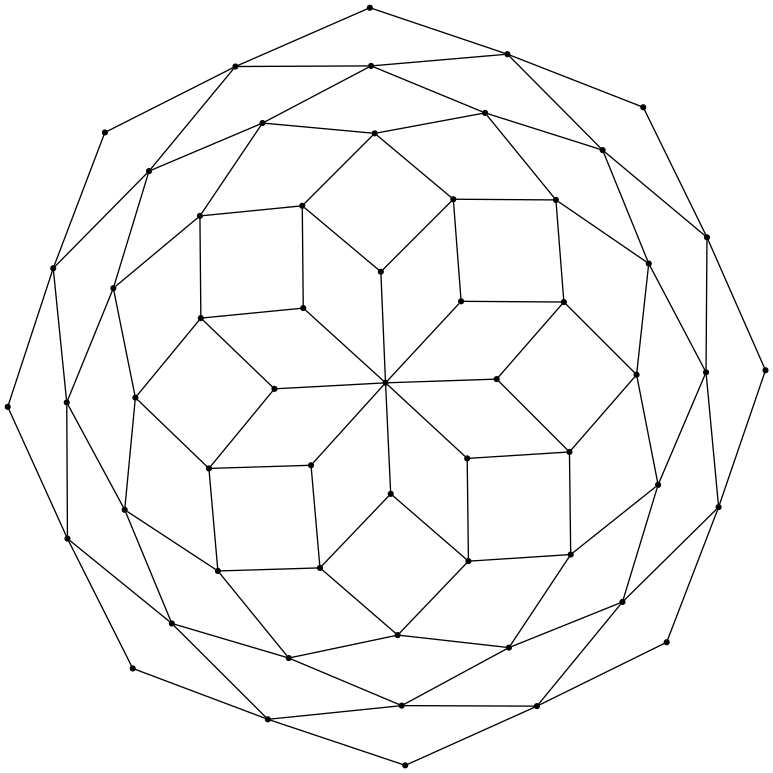
The poset of connected subgraphs on a random tree with 5 vertices
(defun random-tree (n)
(loop for i from 1 below n
collect (list (random i) i)))
(defparameter tree (random-tree 6))
RANDOM-TREE
TREE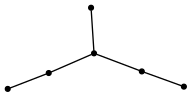
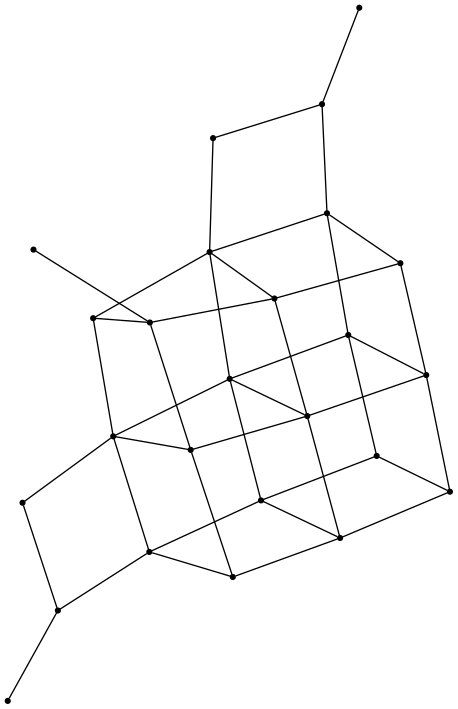
Poset of connected subgraphs of a random connected graph on 4 vertices and 6 edges
(defun take (xs n &optional res)
(if (or (zerop n) (null xs))
(reverse res)
(take (cdr xs) (1- n) (cons (car xs) res))))
(defun pool (n)
(mapcar #'cdr
(sort (loop for i from 0 below (1- n) append
(loop for j from (1+ i) below n collect
(list (random 1.0) i j)))
#'<
:key #'car)))
(defun random-graph (n k)
(let ((edges (pool n))
(tree (random-tree n)))
(do* ((xs edges (remove (car ys) xs :test #'equal))
(ys tree (cdr ys)))
((null ys) (append tree (take xs (1+ (- k n))))))))
(defparameter graph (random-graph 5 6))
TAKE
POOL
RANDOM-GRAPH
GRAPH