Calculating the Diameter and the Radius of a Graph Using Tropic Linear Algebra
Description of the problem:
There is a well-defined notion of distance on a connected graph:
Given two vertices x and y on a graph, the distance between x and y is the length of the shortest path between x and y.
Then we define the eccentricity of a vertex x as the maximum of all possible distances from x
\[ Ecc(x)=max_{y\in V}d(x,y) \]
Then the diameter and radius of the graph is defined as
\[ Diam(G) = max_{x\in V} Ecc(x) = max_{x,y\in V} d(x,y) \]
and
\[ Rad(G) = min_{x\in V} Ecc(x) = min_{x\in V} max_{y\in V} d(x,y) \]
Today’s post is a amalgamation of my two previous posts: one on eccentricity, radius and diameter of a graph and one on shortest path on a graph using tropic linear algebra. Recall from that post, in tropic linear algebra one replaces multiplication of scalars with addition, and addition of scalars with minimum. So, today’s question is
How do we find the eccentricity of a vertex in a graph using tropic linear algebra?
Tropic multiplication of matrices
Given two matrices of the correct dimensions, say \(a=(a_{ij})\) and \(b=(b_{ij})\), their tropic product is computed as
\[ c_{ij}=min_{k=1,...,N} a_{ik}+b_{kj} \]
Adjacency matrix of a graph
Given a graph G=(V,E) where |V|=n, one can represent G using an n×n matrix \(a=(a_{ij})\) as follows: for every vertex i,j=1,…,n, if there is an edge between i and j then set the \(a_{ij}=a_{ji}=1\), and set it +∞ if there is no such an edge. Loops (self connecting edges) have weight 0.
The tropic powers of the adjacency matrix
If we multiply the adjacency matrix \(a\) with itself tropically, we find the price of length 2 paths between vertices. Here the price of each edge is 1. If we multiply \(a\) with itself (n−1) times we would find the length of the cheapest path between any two vertices. This is an easy application of the pigeon hole principle: the longest path one can write without loops or cycles can be of length n−1 in a graph with n vertices.
So, maximum of each colon in the (n−1)-st tropic power of \(a\) will give us the eccentricity of the corresponding vertex.
An implementation in Common Lisp
First, I am going to need a function that converts a graph given as a list of edges to an adjacency matrix:
(defun vertices (G)
(remove-duplicates (sort (reduce #'append G) #'<)))
(defun adjacency-matrix (G)
(let* ((n (1+ (reduce #'max (vertices G))))
(a (make-array (list n n) :initial-element SB-EXT:SINGLE-FLOAT-POSITIVE-INFINITY)))
(dolist (edge G)
(setf (aref a (car edge) (cadr edge)) 1)
(setf (aref a (cadr edge) (car edge)) 1))
(dotimes (i n a)
(setf (aref a i i) 0))))
VERTICES
ADJACENCY-MATRIXNow, here is the code for the tropic product of two matrices.
(defun tropic-mm (xs ys)
(let* ((n (array-dimension xs 1))
(m (array-dimension ys 1))
(k (array-dimension ys 0))
(r (make-array (list n m) :initial-element 0)))
(dotimes (i n r)
(dotimes (j m)
(setf (aref r i j)
(loop for ell from 0 below k minimizing
(+ (aref xs i ell) (aref ys ell j))))))))
TROPIC-MMAs for taking powers, we are going to need
(defun tropic-pow (xs n &optional carry)
(cond ((= n 1) (reduce #'tropic-mm (cons xs carry)))
((evenp n) (tropic-pow (tropic-mm xs xs) (/ n 2) carry))
(t (tropic-pow (tropic-mm xs xs) (floor n 2) (cons xs carry)))))
TROPIC-POWThe function below returns the eccentricities of vertices as a list:
(defun eccentricities (G)
(let* ((A (adjacency-matrix G))
(n (array-dimension A 0))
(result (tropic-pow A (1- n))))
(loop for i from 0 below n collect
(loop for j from 0 below n maximizing
(aref result i j)))))
ECCENTRICITIESThe radius and the diameter then are given by the following function:
(defun diam-rad (G)
(let ((r (eccentricities G)))
(cons (reduce #'max r) (reduce #'min r))))
DIAM-RADLet us test it on a random graph
(defun random-graph (n m k)
(remove-if
(lambda (x) (= (car x) (cadr x)))
(remove-duplicates
(mapcar (lambda (x) (sort x #'<))
(loop repeat (floor m k) append
(loop repeat k collect
(list (random n) (+ (random n) k)))))
:test #'equal)))
(defvar G (random-graph 12 45 5))
RANDOM-GRAPH
G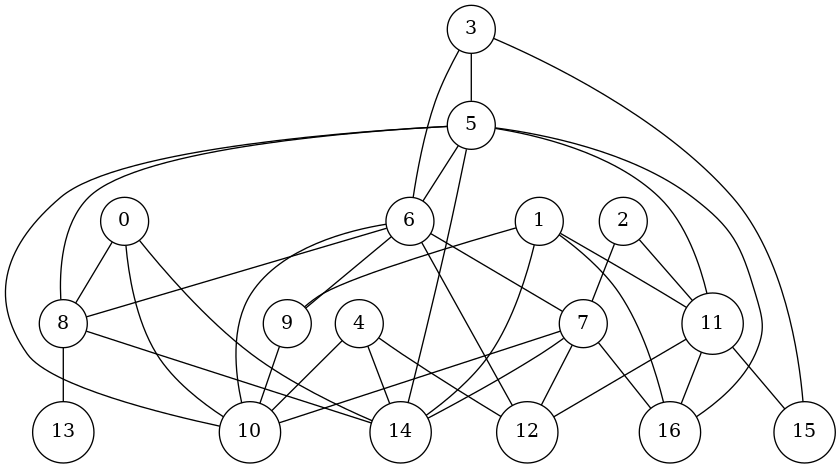
Here are the eccentricities, the diameter and the radius:
(mapcar #'cons (vertices G) (eccentricities G))
(diam-rad G)
((0 . 4) (1 . 3) (2 . 4) (3 . 3) (4 . 4) (5 . 2) (6 . 2) (7 . 3) (8 . 3)
(9 . 3) (10 . 3) (11 . 3) (12 . 3) (13 . 4) (14 . 3) (15 . 4) (16 . 3))
(4 . 2)