Puzzles and Group Theory

Description of the problem

The classical 15-puzzle is a 4x4 square board containing 15 tiles. Each tile is labeled uniquely by numbers from 1 to 15. The empty tile can be 16 different places. The empty slot moves around, and permutes the other tiles. I am going to say that two configurations are equivalent if they can be obtained from each other by doing these permissible permutations.

Unlike the original puzzle, for today’s problem I am going to assume the 4x4 grid is toroidal, i.e. the vertical edges are identified, and so are the horizontal edges. For example the following configurations are the same on such a toroidal grid.

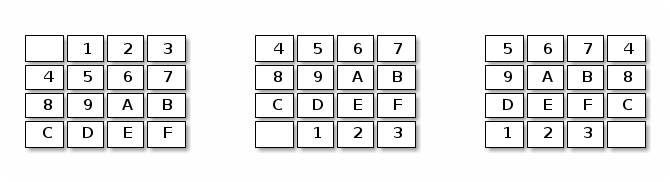
Now, we have only two moves: the horizontal shift followed by normalization

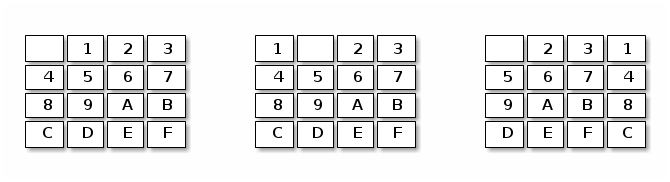
and the vertical shift followed by normalization

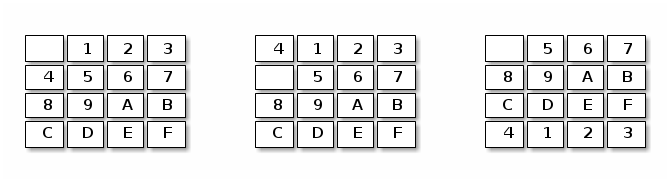
Today’s question is: for this toroidal 15 puzzle, how many non-equivalent configurations are there.

Group theory

If you look closely, these configurations are certain permutations (reorderings) of the hexadecimal digits. These permutations are

(0 2 3 1 5 6 7 4 9 A B 8 D E F C) and (0 5 6 7 8 9 A B C D E F 4 1 2 3)

The set of all permutations of these 16 letters form a group: the symmetric group on 16 letters. The number of elements in this group is very large 16! = 20922789888000. However, these two permutations generate a far smaller number of permutations.

Notice that by assuming the grid is toroidal, and normalizing the coordinate system (observe that in this coordinate system 0 does not move), we reduced the group to the symmetric group on 15 letters.

Before I do any calculation, I need to represent the permutations above using the cycle representation:

(123)(4567)(89AB)(CDEF) and (159D)(26AE)(37BF)(48C)

Computations

For the computations today I am going to use GAP. I need to calculate the number of elements in the subgroup of the symmetric group on 15 letter generated by these two permutations:

gap> K:=Group((1,2,3)(4,5,6,7)(8,9,10,11)(12,13,14,15),(1,5,9,13)(2,6,10,14)(3,7,11,15)(4,8,12));
Group([ (1,2,3)(4,5,6,7)(8,9,10,11)(12,13,14,15), (1,5,9,13)(2,6,10,14)(3,7,11,15)(4,8,12) ])
gap> Q:=Order(K);
1307674368000
gap> Q = Factorial(15);
true

The result indicates in this toroidal 15-puzzle all configurations are equivalent.

The 3-D version of the toroidal puzzle

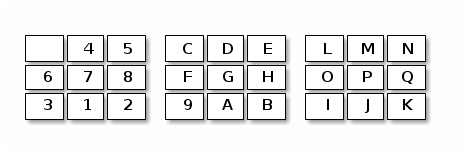
In the 3-D version the toroidal game of size 3x3x3 there are 3 generators:

which corresponds to the permutation

(12)(345)(678)(9ab)(cde)(fgh)(ijk)(lmn)(opq)

Then we have the following generator

which corresponds to

(147)(258)(36)(582)(9cf)(adg)(beh)(ilo)(jmp)

And finally

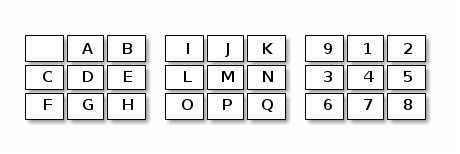
which corresponds to

(1aj)(2bk)(3cl)(4dm)(5en)(6fo)(7gp)(8hq)(9i)

And here is the computation

gap> G := Group((1,2)(3,4,5)(6,7,8)(9,10,11)(12,13,14)(15,16,17)(18,19,20)(21,22,23)(24,25,26), (1,4,7)(2,5,8)(3,6)(9,12,15)(10,13,16)(11,14,17)(18,21,24)(19,22,25), (1,10,19)(2,11,20)(3,12,21)(4,13,22)(5,14,23)(6,15,24)(7,16,25)(8,17,26)(9,18));
Group([ (1,2)(3,4,5)(6,7,8)(9,10,11)(12,13,14)(15,16,17)(18,19,20)(21,22,23)(24,25,26), (1,4,7)(2,5,8)(3,6)(9,12,15)(10,13,16)(11,14,17)(18,21,24)(19,22,25), (1,10,19)
(2,11,20)(3,12,21)(4,13,22)(5,14,23)(6,15,24)(7,16,25)(8,17,26)(9,18) ])
gap> Factorial(26) = Order(G);
true

Again, all configurations are equivalent.