Generating Uniformly Random Connected Graphs

Description of the problem

Today, I’d like to expand on an old post. In that post I gave a simple algorithm and the corresponding lisp code that generates a uniformly random tree on nn vertices. Today, I’ll extend the code to generate a uniformly random connected graph on n vertices.

The main idea

The main idea is to get a uniformly random edge from the whole list of unused edges after we get a uniformly random tree on n vertices.

An implementation

First, I need a utility function that gets the first nn terms in a list.

(defun take (xs n &optional res)
  (if (or (zerop n) (null xs))
      (reverse res)
      (take (cdr xs) (1- n) (cons (car xs) res))))
TAKE

The following function creates all possible edges on the vertex set \({0,\ldots,n−1}\) and then randomly sorts them.

(defun get-the-pool (n)
   (mapcar #'cdr
           (sort (loop for i from 0 below (1- n) append
                      (loop for j from (1+ i) below n collect
                           (list (random 1.0) i j)))
                 #'<
                 :key #'car)))
GET-THE-POOL

I am re-using the following code from my earlier random tree post:

(defun random-tree (n)
  (loop for i from 1 below n collect
       (list (random i) i)))
RANDOM-TREE

Now, the code for the uniformly random connected graph:

(defun get-random-connected-graph (n)
  (let ((pool (get-the-pool n))
        (tree (random-tree n))
        (k (random (floor (- (* n (1- n)) (1- n)) 2))))
    (do* ((xs pool (remove (car ys) xs :test #'equal))
          (ys tree (cdr ys)))
         ((null ys) (append tree (take xs k))))))
GET-RANDOM-CONNECTED-GRAPH

We first get the pool of edges in random order. Then we generate a random tree. This is the key for connectedness since every connected graph has a spanning tree. Then we remove the edges in the randomly generated tree from the pool of edges, and finally we get a random number of edges from the pool to finalize our random graph. I set that number to be between 0 and the half of the remaining edges to get something that I can display.

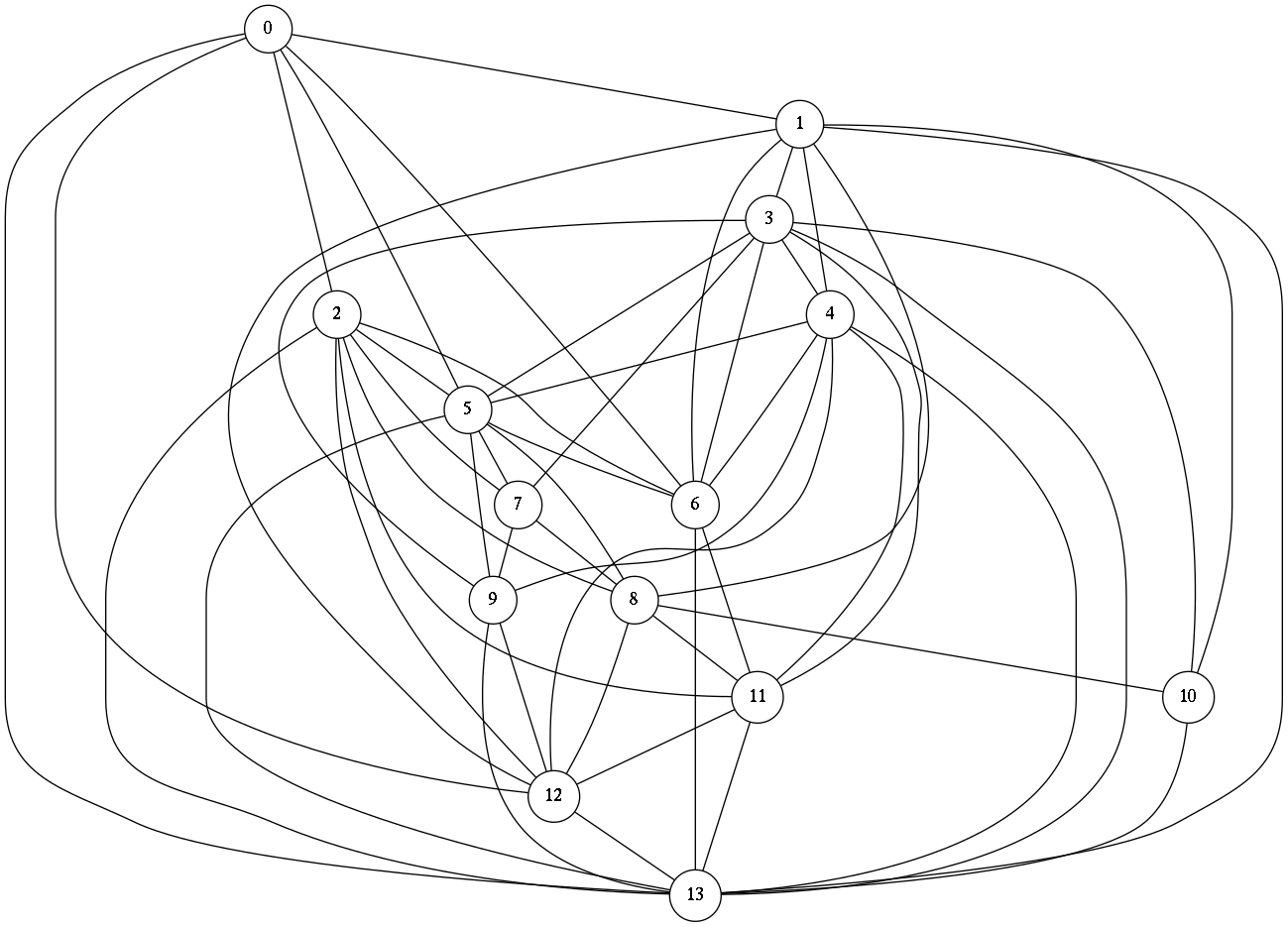
Let us test our code: a random connected graph on 14 vertices.

(defparameter G (get-random-connected-graph 14))
G