Conjugate Partitions

Description of the problem

An unordered \(k\)-partition of \(n\) is an ordered sequence of integers \(n_1 \leq \cdots \leq n_k\) such that \(n = \sum_{i=1}^k n_i\). We can picture such a partition as boxes stacked on top of each other:

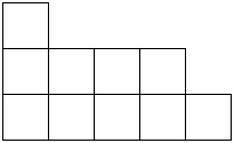
When we read the diagram above we can view it as a \(3\)-partition of \(10\) as \(1\leq 4\leq 5\). But we can also read it as a \(5\)-partition of 10 as \(1\leq 2\leq 2 \leq 2\leq 3\). This is called the conjugate partition.

Today, I am going to describe a short recursive algorithm which calculates the conjugate partition of a given partition.

Algorithm

Given a \(k\)-partition of \(n\), the number of terms in the conjugate partition is given by the largest number in that partition. Then largest number in the conjugate partition is the length of the original partition. Once we observe that we can write our algorithm recursively

Algorithm Dual
Input: xs which is a k-partition n
Output: the conjugate partition of xs
Begin
  If xs is null then
     Return an empty list
  Else
     Let k be min(xs)
     Let n be length(xs)
     Let zs be the list containing k many n's
     Let ys be the empty list
     For each x in xs
         If x > k then
            Append x - k to ys
         End
     End
  End
  Return the list after appending Dual(ys) to zs 
End

Implementation

Here is an implementation

(defun dual (xs &optional ys)
  (if (null xs)
      ys
      (let ((k (car xs))
            (n (length xs)))            
         (dual (remove-if #'zerop
                          (mapcar (lambda (x) (- x k))
                                  xs))
               (append (loop repeat k collect n) ys)))))
DUAL

Let us test it on the example whose picture I gave above:

(dual '(1 4 5))
(1 2 2 2 3)

(dual (dual '(1 4 5)))
(1 4 5)

Now, let us test it on a large random partition:

(defvar xs (sort (loop repeat 20 collect (1+ (random 10))) #'<))
XS

xs
(1 1 1 2 2 2 3 4 5 5 5 7 8 8 9 9 9 9 9 9)

(dual xs)
(6 8 9 9 12 13 14 17 20)

(dual (dual xs))
(1 1 1 2 2 2 3 4 5 5 5 7 8 8 9 9 9 9 9 9)

Efficiency Issues

Rainer Joswig correctly commented saying the original implementation wasn’t very efficient.  Since then I made few modifications making the implementation above even simpler.  He gave several different implementations, one of which is recursive.  Check out his versions here.