Basic Data Analysis with CL without Frameworks

I was looking at CLML Tutorial.  CLML seems to be a well-designed and comprehensive machine learning library that can do a lot of things from time series analysis to neural networks.

I am against using heavy frameworks for doing anything. I think libraries too should confine themselves to do one thing well.  If your language is well-designed, like common lisp, combining specialized libraries to do even the most difficult and complicated tasks become possible after careful design.

Today’s task, then, is to use common lisp and relatively familiar common lisp libraries to achieve what has been done in the aforementioned tutorial.  Instead of using babel and org mode, I will do this post on cl-jupyter.

Let’s get to it

First, let us define our package and load our libraries:

(mapc #'require '(:drakma :cl-ppcre :lla :gsll))

(defpackage #:my-test
    (:use #:cl)
    (:import-from #:lla svd svd-u svd-d svd-vt dot)
    (:import-from #:grid column row)
    (:import-from #:cl-ppcre split)
    (:import-from #:drakma http-request))

(in-package #:my-test)
#<PACKAGE "MY-TEST">

Now, let me define a function to get the data from the web from a given URL:

(defun slurp-data (URL &optional (separator ","))
    (mapcar (lambda (x) (mapcar #'read-from-string (split separator x)))
            (split "\n+" (http-request URL))))
SLURP-DATA

OK. Let us get the data:

(defparameter raw (slurp-data "http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data"))
(list (car raw) (cadr raw))

((1 14.23 1.71 2.43 15.6 127 2.8 3.06 0.28 2.29 5.64 1.04 3.92 1065)
 (1 13.2 1.78 2.14 11.2 100 2.65 2.76 0.26 1.28 4.38 1.05 3.4 1050))

We don’t need the first column since it tells us the class.  

(defparameter wine (mapcar #'cdr raw))

WINE

I am going to apply singular value decomposition on the data.  For that I am using the LLA library.  The library requires that the data is in the form of a 2d-array:

(defparameter matrix
    (let ((n (length wine))
          (m (length (car wine))))
       (make-array (list n m) :initial-contents wine)))

(defparameter svd-result (svd matrix))

SVD-RESULT

Let us check the singular values:

(slot-value (svd-d svd-result) 'cl-num-utils.matrix::elements)

#(10886.66990656052d0 493.56204760867354d0 57.1488432147479d0
  30.100125524021887d0 18.54281551828445d0 14.46302059358436d0
  11.036037653318322d0 5.289890187623465d0 4.456588316877591d0
  3.575271453862534d0 2.6012217367795545d0 1.9868082509451046d0
  1.2139139647789066d0)

Result indicates that the first two singular vectors should be just enough.   In order to project our 14D vectors to 2D vectors, I am going to need a dot-product. The LLA library already has that.  After I project the data-points, I will combine the wine-class data with the projected vector.  The result will be written in a file which I will use with gnuplot.

(let* ((vecs (mapcar (lambda (i) (row (svd-u svd-result) i)) (list 0 1)))
       (data (mapcar (lambda (x) (coerce x 'vector)) wine))
       (class (mapcar #'car raw))
       (projected-data 
           (mapcar (lambda (x y) (cons y (mapcar (lambda (z) (dot z x)) vecs))) 
                  data 
                  class)))
   (with-open-file (out "data.csv" :direction :output :if-does-not-exist :create :if-exists :supersede)
       (format out "~{~{~5,4F~^, ~}~%~}" projected-data)))

NIL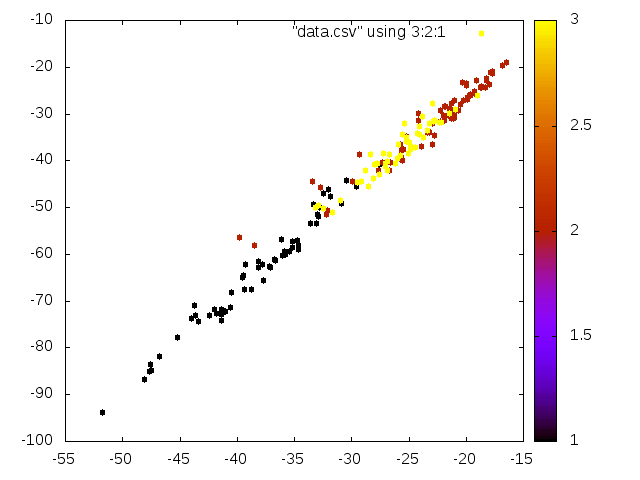

Analysis

Good separation between class 1 and class 2 wines, and class 3 is scattered in between.  Looking at the data, one might have used only the most dominant vector to achieve the same separation.

Unlike the CLML Tutorial, I didn’t normalize the data because the separation was much worse after a normalization.

So, there you have it. “Look ma! No frameworks.”