Eigen-values of the Laplacian and Connected Components of a Graph

Description of the problem

This post is inspired by a post I saw at John D. Cook’s blog. John observes that the second smallest eigen-value of the Laplacian gives us important information about the connectivity of the graph. The eigen-values tell more, of course. See for example Fan Graham’s excellent survey on the subject.

Today, I will write my implementation of the experiment on testing the second smallest eigen-value of the Laplacian of a graph in common lisp.

Implementation

First, I am going to need two utility thunks: the first is a macro,

 (defmacro -> (x &rest forms)
   (dolist (f forms x)
     (if (listp f)
         (setf x (append (list (car f) x) (cdr f)))
         (setf x (list f x))))) 
->

while the other is a function.

 (defun group-by (xs &optional (fn (lambda (x) x)))
   (let (res)
     (dolist (x xs res)
       (let* ((y (funcall fn x))
              (z (cdr (assoc y res))))
         (if (null z)
             (push (cons y (list x)) res)
             (setf (cdr (assoc y res))
                   (cons x z)))))))
GROUP-BY

I am going to use the threading macro -> for compositions of functions on a single value, while I need group-by to group values in a list using a criterion, in this case the identity function.

I have been using the set of edges as a representation of a graph. For example:

(defvar G '((0 1) (0 2) (1 2) (1 3) (3 4)))
G

represents the graph whose picture can be drawn as

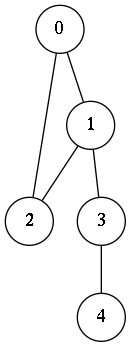
First, let us get the list of vertices and their degrees from a given graph.

(defun degrees (G)
   (mapcar (lambda (x) (cons (car x) (length (cdr x))))
           (group-by (reduce #'append G)  (lambda (x) x))))
DEGREES

For the graph we had above, the result is going to be

(degrees G)
((4 . 1) (3 . 2) (2 . 2) (1 . 3) (0 . 2))

Next, a function that returns the Laplacian of a given graph:

(defun laplacian (G)
  (let* ((degs (degrees G))
         (n (1+ (reduce #'max (mapcar #'car degs))))
         (res (make-array (list n n) :initial-element 0)))
    (dolist (x degs)
      (setf (aref res (car x) (car x)) (cdr x)))
    (dolist (e G res)
      (decf (apply #'aref res e))
      (decf (apply #'aref res (reverse e))))))
LAPLACIAN

Now, let me define our experiment function:

(defun experiment (G)
  (-> G
      laplacian
      cl-num-utils:hermitian-matrix
      lla:eigenvalues
      (sort #'<)
      (aref 1)))
EXPERIMENT

And our experiment

(experiment G)
0.5188056959079844d0

For the next experiment, I am going to need a random disconnected graph:

(defun random-graph (n m a b)
   (remove-duplicates
       (loop repeat n collect
           (let* ((x (+ b (random m)))
                  (y (+ 1 (random a) x)))
               (list x y)))
       :test #'equal))
RANDOM-GRAPH

Here is our random graph:

(defvar H  (append (random-graph 16 4 3 0)
                   (random-graph 25 5 3 8)))
H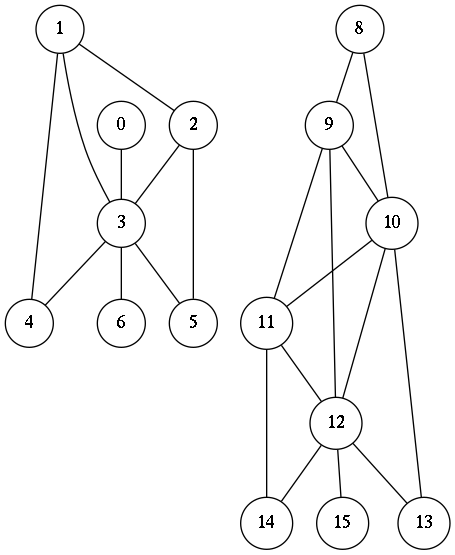

And, the result of the experiment on this graph:

(format nil "~4,3f" (experiment H))
.000