Dual Graphs
Description of the problem
Assume we have a graph G=(V,E) where V is just a finite set of vertices and E is just a collection of (unordered) pairs of vertices we call edges. From this graph, we form a new graph G′ as follows: the set of vertices is the set E of edges of G. We put an edge between e and f if e and f share a common vertex in G. Today I am going to give you a lisp program which calculates the dual graph of a given graph.
There is a notion of a dual graph of a planar graph which is different than this dual.
Implementation
I have been using a list of pairs of vertices to denote graphs. I will continue to do so. So, given a graph G we will use a pair of nested loops over the list of edges to form the new graph.
(defun dual (G)
(let (res
(n (length G)))
(dotimes (i (1- n) res)
(dotimes (j (- n i 1))
(let ((e (nth i G))
(f (nth (+ i j 1) G)))
(if (intersection e f)
(push (list e f) res)))))))
DUALLet us test. But before the test, I am going to need a random graph.
(defun random-graph (n m k)
(remove-duplicates
(loop repeat m collect
(let* ((a (random n))
(b (+ (random k) a 1)))
(list a b)))
:test #'equal))
RANDOM-GRAPH
(defvar G (random-graph 4 8 3))
G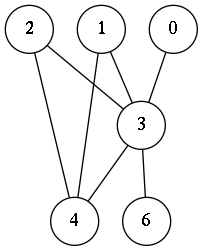
and our test:
(defvar H (dual G))
H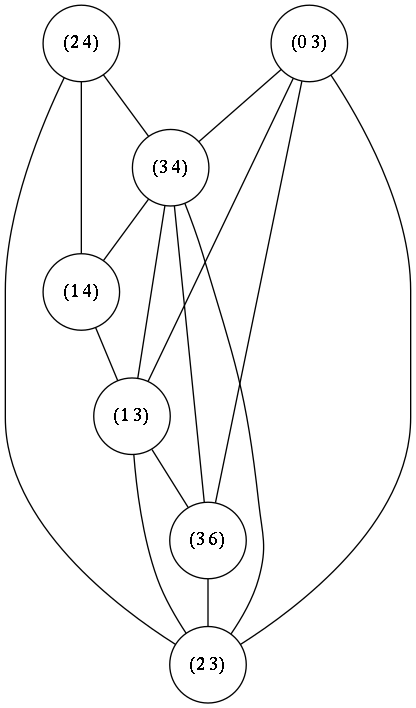
How about the double dual?
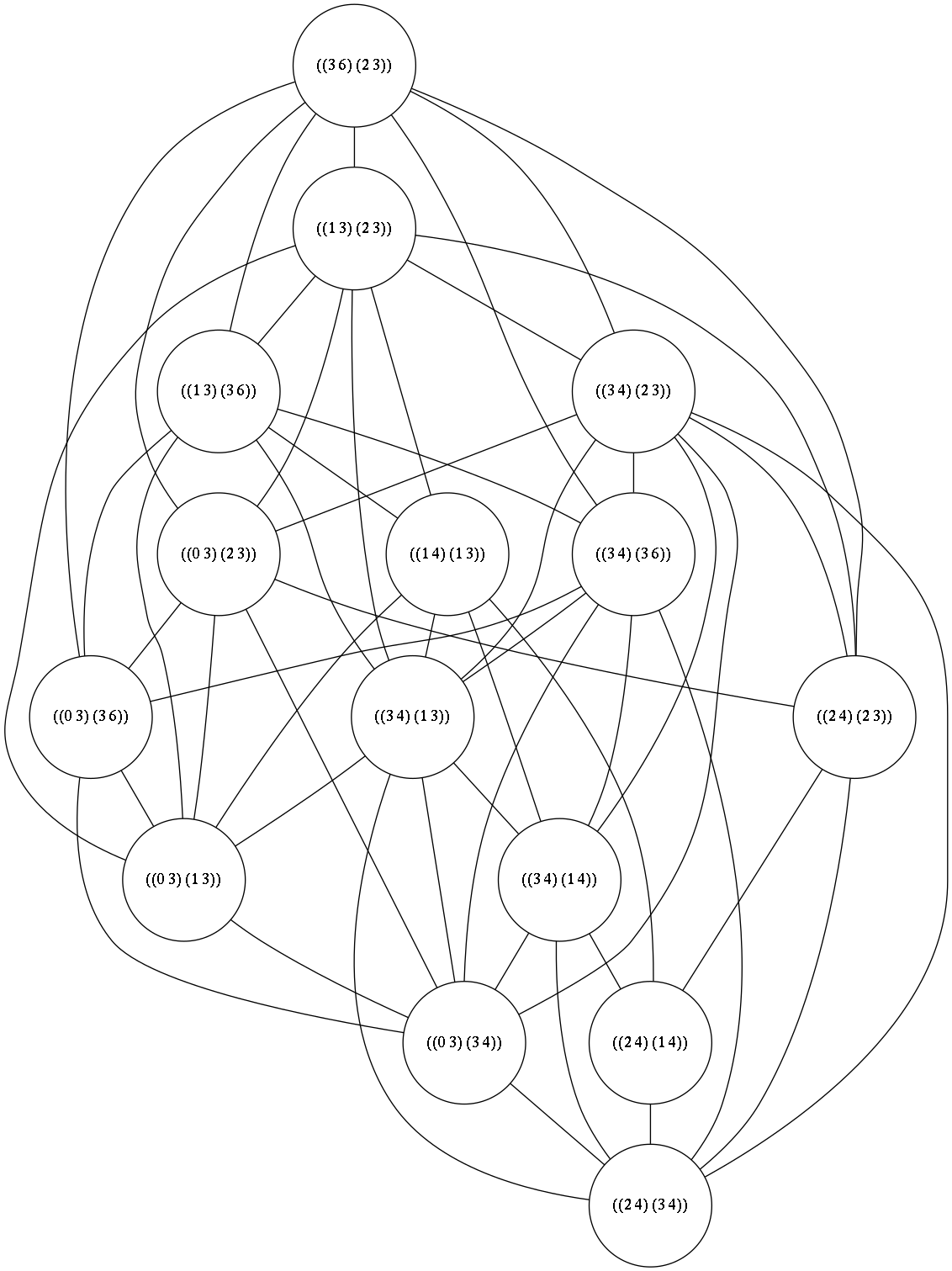
As you can notice, this is not the original graph. The problem arises because in the double dual, vertices are duplicated. The number of duplicates in the double dual is exactly as many as the degree of that particular vertex.