Cheapest Paths via Tropic Matrices
I wrote another blog post on the following problem but I have slight improvements. It is worth another post.
Description of the problem
Assume we have an undirected graph \(G=(V,E)\) where each edge is associated with a cost \(\omega :E \to \[0,\infty)\). Given two vertices \(a,b\in V\), our aim today is to find the cheapest path between \(a\) and \(b\).
Tropic matrices
Consider the symmetric square matrix \(\Omega = (\omega(v,w))_{vw}\) whose rows and columns are labeled by vertices. Then the minimal costs of 1-step paths between vertices is given by \(\Omega\) itself. If we were to think of the minimal costs of 2-step paths between vertices then we would need \[ c^{(2)}_{ij}=ω_{ij} \wedge \bigwedge_{k\in V} \omega_{ik} + \omega_{kj}\] where I use the notation \(a\wedge b\) for \(\min(a,b)\). Inductively, the costs of cheapest paths of length less or equal to \(n+1\) are calculated by \[ c^{(n+1)}_{ij} = c^{(n)}_{ij}\wedge \bigwedge_{k\in V} c^{(n)}_{ik} + \omega_{kj} \] If you have seen my previous post on Hidden Markov Models you will realize that I am doing matrix multiplication in the tropic ring over the positive real numbers.
An implementation
I will take the tropic matrix multiplication I defined in my previous post but I need to modify the function since minimum must be taken of paths of shorter lengths too.
(defun tropic-mult (a b)
(let ((n (array-dimension a 0))
(m (array-dimension b 1))
(o (array-dimension a 1)))
(make-array
(list n m)
:initial-contents
(loop for i from 0 below n collect
(loop for j from 0 below m collect
(car (sort (cons (aref a i j)
(loop for k from 0 below o collect
(cons (append (car (aref a i k))
(cdar (aref b k j)))
(+ (cdr (aref a i k))
(cdr (aref b k j))))))
(lambda (x y) (< (cdr x) (cdr y))))))))))
TROPIC-MULTThe function assumes that each entry is of the form
(path . cost) and when it multiplies two such matrices, it
will concatenate paths and evaluate costs tropically. It will also
include a in the comparisons to look at paths of shorter
lengths.
I will represent a graph with weighted edges as a list of cons pairs
of the form (edge . cost)
(defvar graph1
(loop for i from 0 below 21 append
(loop for j from (1+ i) below 22 collect
(cons (list j i) (if (zerop (random 8))
(1+ (random 10)))))))
GRAPH1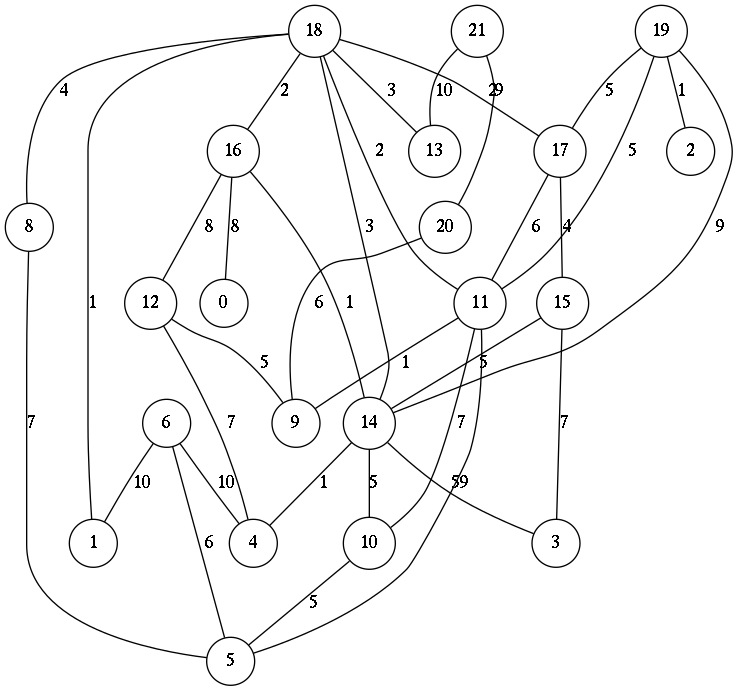
First, I will need a function that converts such a list to a matrix: I will set the weights non-existing edges to a prohibitively large number (in this case it is 10000) which depends on the set of possible weights for the graph at hand.
(defun convert (G)
(let ((n (length (reduce #'union (mapcar #'car G)))))
(make-array
(list n n)
:initial-contents
(loop for i from 0 below n collect
(loop for j from 0 below n collect
(let ((x (or (cdr (assoc (list i j) G :test #'equal))
(cdr (assoc (list j i) G :test #'equal)))))
(cons (list i j) (or x 10000))))))))
CONVERTNow, the following function returns the cheapest path between two
vertices i and j of length less than or equal
to n in a weighted graph G:
(defun cheapest-path (i j n G)
(let ((m (convert G)))
(aref (reduce #'tropic-mult (loop repeat n collect m)) i j)))
CHEAPEST-PATH
(cheapest-path 5 21 7 graph1)
((5 8 18 13 21) . 24)