Hidden Markov Models via Tropic Matrices

I covered some of the material in my previous post, but let me repeat it anyway.

Description of the problem

We have an ordered sequence of observations \(x_1,x_2,\ldots,x_N\) where each observation is labeled from a finite set of classes \(Y\). The probability that an observation \(x\) is labeled as \(y\in Y\) is given by \(p(y\|x)\). We assume that we know the probability distributions for the observations \(p(x)\) and classes \(p(y)\), and the probability \(p(x\|y)\) of seeing the observation \(x\) under the label \(y\). Assume also that we have transition probabilities \(p(y'\|y)\) telling us the probability of seeing class label \(y'\in Y\) right after observing \(y\in Y\).

Our task is to find the labeling scheme \(\ell\colon \{x_1,\ldots,x_N\}\to Y\) of the observations with the maximum likelihood. In other words, we need to maximize \[ \pi(\ell) = \prod_{i=1}^N p(\ell(x_i)\|x_i)p(\ell(x_{i+1})\|\ell(x_i)) \] We set \(p(\ell(x_{N+1})\|\ell(x_N))=1\) to make the product meaningful.

A reduction

Taking the logarithms and expanding we get \[ \log\pi(\ell) = \sum_{i=1}^N \log p(\ell(x_i)\| x_i) + \sum_{i=1}^{N-1} \log p(\ell(x_{i+1})\|\ell(x_i)) \] which then can be simplified as \[ = \sum_{i=1}^N \log p(\ell(x_{i+1})\|\ell(x_i)) + \sum_{i=1}^N \log p(x_i\|\ell(x_i)) + \log p(\ell(x_i)) - \log p(x_i) \] Notice that we can drop \(\log p(x_i)\) terms since they do not depend on \(\ell\). Since logarithms of probabilities lie in \((-\infty,0\]\), we need to minimize the quantity below: \[ -\log\pi(\ell) \sim \tau(\ell) := \sum_{i=1}^N -\log p(\ell(x_{i+1})\|\ell(x_i)) + \sum_{i=1}^N -\log p(x_i\|\ell(x_i)) + \sum_{i=1}^N -\log p(\ell(x_i)) \] Let us rearrange the terms a bit: \[ \tau(\ell) = - \sum_{i=1}^N \log p(x_i\|\ell(x_i)) + \log p(\ell(x_i)) + \log p(\ell(x_i)\|\ell(x_{i-1})) \] by letting \(p(\ell(x_1)\|\ell(x_0))=1\) in the equation.

Tropic semiring

We consider the set of non-negative real numbers \(\mathbb{R}_+ := \[0,\infty)\) together with the operations \(\min\) (which we denote as \(\min(x,y) = x\wedge y\)) and ordinary product. Notice that \[ x + (y\wedge z) = (x+y)\wedge(x+z) \] However, \(\wedge\) does not have a unit and \(0\wedge x = x\wedge 0 = 0\).

One can form matrices in the tropic semi-rng. Assume we have two such tropic matrices \(A_{n\times m} = (a_{ij})\) and \(B_{m\times\ell} = (b_{ij})\) then the product \(C_{n\times\ell} = A\ast B\) has the entries \[ c_{ij} = \bigwedge_{k=1}^m (a_{ik} + b_{kj}) \]

Re-imagining our problem in tropic terms

Let us define matrices \(\omega_i\) for \(i=1,\ldots,n\) as \[ \omega_{jk}(i) = - \log p(x_i\|y_j) - \log p(y_j) - \log p(y_j\|y_k) \] Now, the problem we stated above reduces to calculating the entries of \[ \omega(1)\cdots\omega(n) \] and finding the minimal entry together with the path that produced that entry.

An implementation

Let us start with tropic multiplication of matrices. Our matrices have entries as pairs (path . -log(prob)). Each path at the entry (i j) is a sequence of indices that starts at \(i\) and ends at \(j\). We are going to concatenate paths, and tropic multiply entries coming from negative log terms. The following function takes two matrices of this form and returns their product.

(defun tropic-mult (a b)
   (let ((n (array-dimension a 0))
         (m (array-dimension b 1))
         (o (array-dimension a 1)))
      (make-array
         (list n m)
         :initial-contents 
            (loop for i from 0 below n collect
               (loop for j from 0 below m collect
                  (car (sort (loop for k from 0 below o collect
                                (cons (append (car (aref a i k))
                                              (cdar (aref b k j)))
                                      (+ (cdr (aref a i k))
                                         (cdr (aref b k j)))))
                       (lambda (x y) (< (cdr x) (cdr y))))))))))
TROPIC-MULT

A toy example

Let me test. I will start with something small. Assume I have the following transition probabilities between two states:

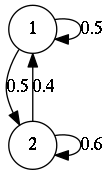
(defvar
   A (make-array
       (list 2 2)
       :initial-contents
         (list (list (cons (list 1 1) (- (log 0.5))) (cons (list 1 2) (- (log 0.5))))
               (list (cons (list 2 1) (- (log 0.4))) (cons (list 2 2) (- (log 0.6)))))))
A
(reduce #’tropic-mult a a a a)
#2A((((1 2 2 2 1) . 2.6310892) ((1 2 2 2 2) . 2.225624))
    (((2 2 2 2 1) . 2.4487674) ((2 2 2 2 2) . 2.0433023)))

The result indicates that the most likely 4-step path is (2 2 2 2 2) from state 2 to state 2, but if we want we have the most likely 4-step path from state 1 and state 1 then we have (1 2 2 2 1)

A real test

For our real test, I am going to need a function that generates the sequence of matrices we going going to multiply. The following function takes 3 inputs:

1. A matrix a of the conditional probabilities \(p(x_i\|y_j)\) of seeing a state \(x_i\) given the label \(y_j\).
2. A matrix b of the probability distribution of the labels \(y_j\)’s
3. A matrix c of transition probabilities \(p(y_j\|y_i)\) from a label \(y_i\) to another label \(y_j\).

and it returns a list of matrices \((\omega(1),\ldots,\omega(m))\).

(defun matrix (a b c)
   (let* ((m (array-dimension a 1))
          (n (array-dimension a 0)))
      (loop for i from 0 below m collect
         (make-array
            (list n n)
            :initial-contents
               (loop for j from 0 below n collect
                  (loop for k from 0 below n collect
                     (cons
                        (list j k)
                        (+ (- (log (aref a j i)))
                           (- (log (aref b j)))
                           (- (log (aref c j k)))))))))))
MATRIX

And our final test:

(let* ((a (make-array
             (list 3 4)
             :initial-contents
               '((0.25 0.25 0.25 0.25)
                 (0.05 0.00 0.95 0.00)
                 (0.40 0.10 0.10 0.40))))
       (b (make-array 3 :initial-contents '(0.5 0.1 0.4)))
       (c (make-array
             (list 3 3)
             :initial-contents
               '((0.75 0.25 0.00)
                 (0.00 0.00 1.00)
                 (0.00 0.00 1.00))))
       (path (mapcar (lambda (x) (position x '(:a :c :g :t)))
                '(:c :t :t :c
                  :a :t :g :t
                  :g :a :a :a
                  :g :c :a :g
                  :a :c :g :t
                  :a :a :g :t
                  :c :a)))
       (matr (matrix a b c)))
   (reduce #'tropic-mult (loop for x in path collect (elt matr x))))
#2A((((0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0) . 61.545197)
     ((0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1) . 62.64381)
     ((0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 2 2 2 2 2 2 2) . 61.66136))
    (((1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0)
      . #.SB-EXT:SINGLE-FLOAT-POSITIVE-INFINITY)
     ((1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1)
      . #.SB-EXT:SINGLE-FLOAT-POSITIVE-INFINITY)
     ((1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2)
      . #.SB-EXT:SINGLE-FLOAT-POSITIVE-INFINITY))
    (((2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0)
      . #.SB-EXT:SINGLE-FLOAT-POSITIVE-INFINITY)
     ((2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1)
      . #.SB-EXT:SINGLE-FLOAT-POSITIVE-INFINITY)
     ((2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2) . 62.896347)))

Now, we see that the most probable path from state 0 to state 2 on these sequence of observations is (0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 2 2 2 2 2 2 2) which agrees with the result obtained in the paper I took this problem from.

An analysis

Comparing the results with my previous post, we see that recursion with no memory leads to the most probable path with a given initial state, while in today’s implementation we find the most probable path with the chosen initial and terminal state which is more desirable.