Finding Cliques in a Graph

Description of the problem

Today’s post is about finding cliques in a graph: A clique in an undirected graph G is a subgraph which is complete. One specific algorithm on finding cliques is a family of algorithms called Bron-Kerbosch Algrithm(s). They were simple enough to implement.

The algorithm

Algorithm Bron-Kerbosch
Input: Three subsets of vertices P, X and R
Output: A family of cliques defined as subsets of the set of vertices
Begin
   if P and X are both empty:
       report R as a maximal clique
   end if
   for each vertex v in P:
       N <- set of neighbors of v
       call Bron-Kerbosch with R union {v}, P intersection N, X intersection N
       P <- P \ {v}
       X <- X union {v}
   end for
End

An implementation in Common Lisp

The pseudo-code of the first variation was easy enough to translate to Common Lisp. I will assume (as I did in most of the posts on graphs on this blog) that a graph is given as a list of edges where each edge is a list of pairs of vertices.  

(defun cliques (graph)
    (let* ((vertices (remove-duplicates (reduce #'append graph)))
           (neighbors
            (loop for x in vertices collect
                (let (res)
                   (dolist (v vertices (cons x (remove-duplicates (sort res #'<))))
                      (if (member (sort (list v x) #'<)graph :test #'equal)
                          (push v res))))))
           (cliques nil))
      (labels ((bron-kerbosch (p r x)
                 (if (and (null p) (null x))
                     (push r cliques))
                 (mapl (lambda (q)
                         (let* ((v (car q))
                                (n (cdr (assoc v neighbors))))
                           (bron-kerbosch (intersection q n)
                                          (union (list v) r)
                                          (intersection x n))
                           (setf x (cons v x))))
                       p)))
         (bron-kerbosch vertices nil nil))
      (sort (mapcar (lambda (x) (sort x #'<)) cliques)
            (lambda (x y) (> (length x) (length y))))))
CLIQUES

I implemented neighbors as an assoc list instead of implementing it as a function to save time. Also, the for loop inside the recursive core was using P with one element removed each time. This was the perfect use case for mapl.

Let us test it on a complete graph:

(let ((G (loop for i from 0 to 9 append
              (loop for j from (1+ i) to 10 collect
                 (list i j)))))
     (cliques G))
((0 1 2 3 4 5 6 7 8 9 10))

and now on a random graph:

(defun random-graph (n m k)
    (remove-if
     (lambda (x) (= (car x) (cadr x)))
     (remove-duplicates 
      (sort (mapcar (lambda (x) (sort x #'<))
                    (loop repeat (floor m k) append
                         (loop repeat k collect
                              (list (random n) (+ (random n) k)))))
            (lambda (a b) (or (< (car a) (car b)) (and (= (car a) (car b)) (< (cadr a) (cadr b))))))
      :test #'equal)))
RANDOM-GRAPH
(defvar G (random-graph 10 100 3)) 
G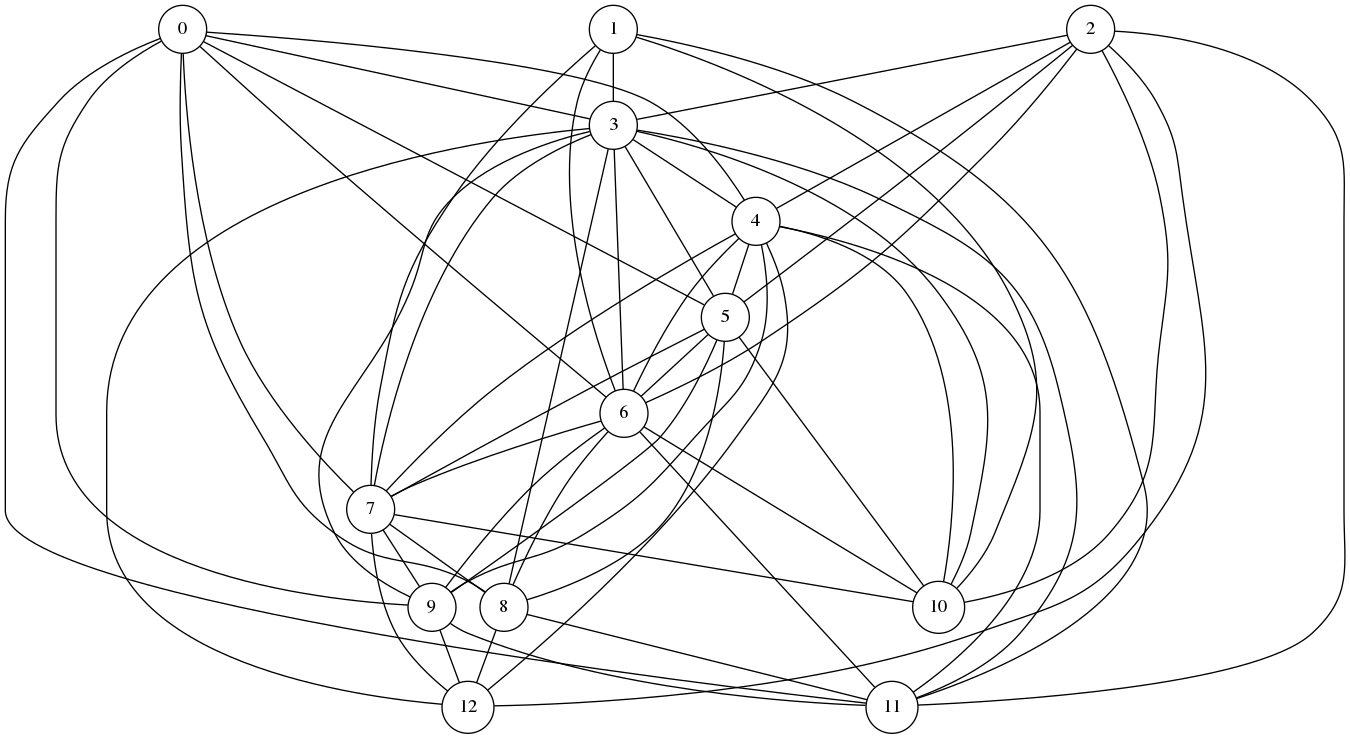

(cliques G)
((0 3 4 5 6 7 9) (3 4 5 6 7 10) (2 3 4 5 6 10) (0 3 5 6 7 8) (0 3 4 6 9 11)
 (3 4 7 9 12) (2 3 4 6 11) (1 3 6 7 10) (0 3 6 8 11) (3 7 8 12) (2 3 4 12)
 (1 3 6 11))