Hamming Distance and Double Hashing

Description of the problem

I will consider the space of bitstrings of a fixed length as a metricspace \((X,d)\) where the metric is given by the Hammingdistance \(d(x,y)\) which calculates the number of sites on which two bitstrings \(x\) and \(y\) differ.

Now, I will consider a hash function as a self map \(f\colon X\to X\).

The main objects of interest for today’s post is the distributions of the numbers \[d(f(f(x)),f(x))\] for every \(x\). I would like compare the distributions of numbers with \[ {d(f(x),x)}\].

Hamming distances

I am going to use some code from last two posts, which are not shown here.

Let us see the results for MD5:

    Two-sample Kolmogorov-Smirnov test

data:  as.matrix(X[, 1]) and as.matrix(X[, 2])
D = 0.0167, p-value = 0.07134
alternative hypothesis: two-sided

There is no discernible statistical difference.

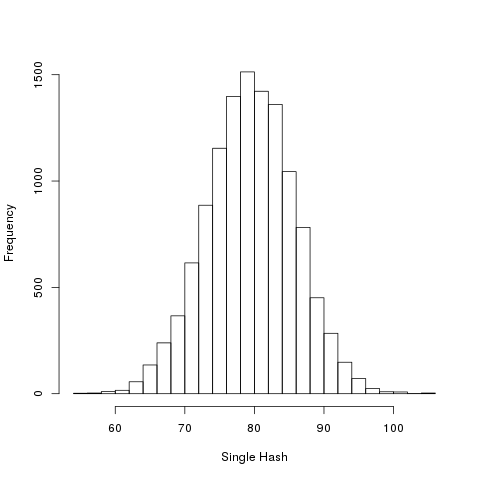
Now, the results for SHA1:

    Two-sample Kolmogorov-Smirnov test

data:  as.matrix(X[, 1]) and as.matrix(X[, 2])
D = 0.0128, p-value = 0.2764
alternative hypothesis: two-sided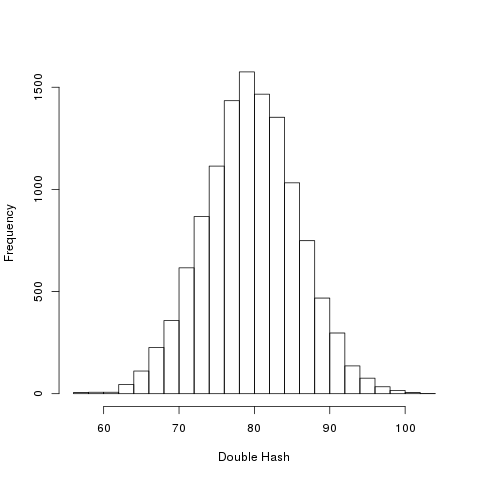

Again, there is no discernible statistical difference.