Curve Fitting is a Gram-Schmidt Reduction

One of the things you can do with time series data is to fit a curve (say trend, or average, or natural cycles) and then analyze the residue. The subject is studied to death out there, but I discovered a neat trick that I would like to share.

Assume we have a function \(f(x)\), but we want to express it in terms of a (finite) collection of other functions \(f_1(x),\ldots,f_n(x)\). In the discrete version of the same problem we have a set of data points \((x_1,\ldots,x_N)\) and we want a collection of data points \((y^{(i)}_1,\ldots,y^{(i)}_{M_i})\) to fit. If without loss of generality, we assume each \(M_i\) is the same as \(N\), we can use the Gram-Schmidt Process to get the data fit. The idea is simple enough to implement, and there is already a nice paper on the subject.

Code

The only non-trivial part of the code is the Gram-Schmidt reduction:

(defun gram-schmidt (xs &optional tail)
   (labels ((dot (a b) (reduce #'+ (mapcar #'* a b))))
      (if (null (cdr xs))
         (cons (car xs) tail)
         (destructuring-bind
              (y . ys) xs
           (gram-schmidt
              (mapcar (lambda (z)
                         (let ((c (/ (dot y z) (dot y y))))
                            (mapcar (lambda (i j) (- i (* c j))) z y)))
                      ys)
              (cons y tail))))))
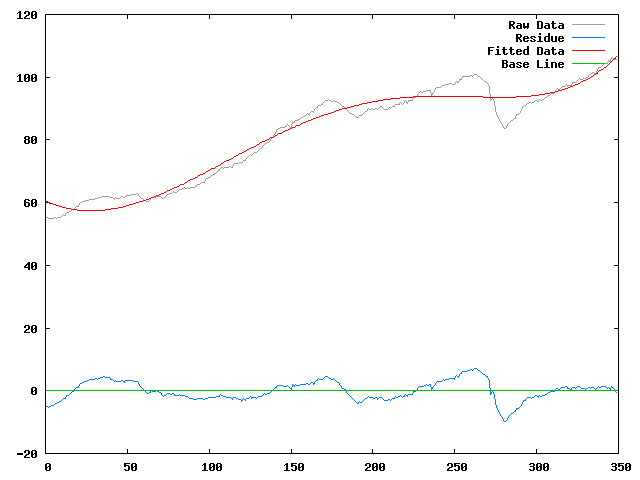
GRAM-SCHMIDT

The data I am going to use is from Federal Reserve. I am going to look at the total production index from March 1986 to February 2015. The data need to be extracted from the file I downloaded. I used

grep grep B50001 ip_sa.txt | grep -v : | awk '{ for(i=3;i<15;i++) { print $i; } }' > total_index.csv

to extract the pieces I needed. I am going to load the data into a variable called *raw-data*

(defvar *raw-data*
   (with-open-file (in "total_index.csv" :direction :input)
      (do* ((item (read-line in nil) (read-line in nil))
            (res (list item) (cons item res)))
           ((null item) (mapcar #'read-from-string (reverse (cdr res)))))))
*RAW-DATA*

I am going to fit a degree 5 polynomial with the degree 4 monomial missing onto the data.

(defun residues (raw degrees)
   (labels ((poly (k n) (loop for i from 0 below n collect (expt i k))))
      (let ((n (length raw)))
         (car (gram-schmidt (reverse (cons raw (mapcar (lambda (x) (poly x n)) degrees))))))))
RESIDUES


(defvar *residue* (residues *raw-data* '(0 1 2 3 5)))
*RESIDUE*

Let us see the results: