Collatz-type Conjectures (Continued)

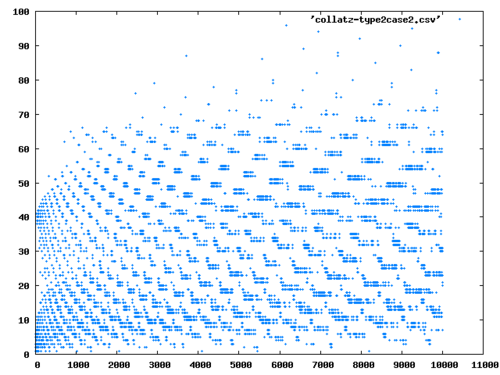
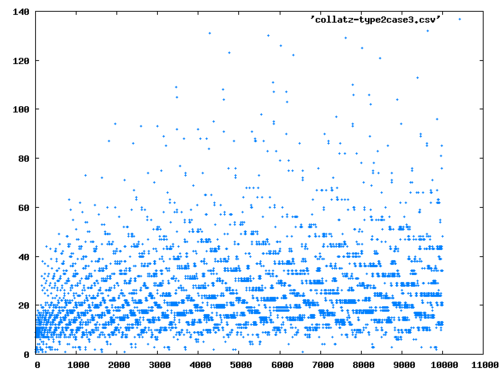
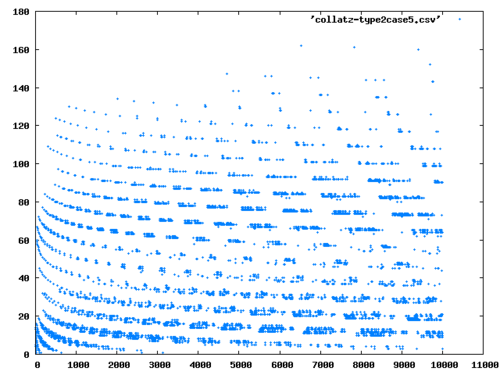
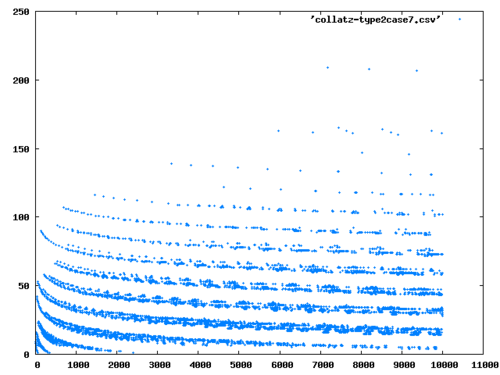
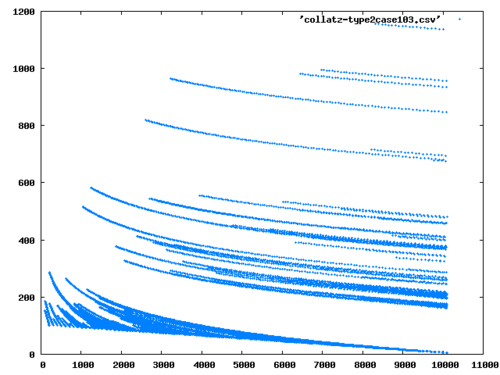
Today’s post is going to be short. I would like to show collatz lengths of natural numbers with different values of \(p\).

Let us recall: we have two functions

(defun f (n p)
   (if (zerop (mod n p))
      (f (/ n p) p)
      n))
F

(defun g (n p)
   (if (zerop (mod n p))
      (f (/ n p) p)
      (f (+ (* n p) n p (- (mod n p))) p)))
G

From this we calculate lengths of the recursive sequence \(a_{n+1} = g_p(a_n)\). We are going to terminate the recursive sequence when \(a_n\) hits 1, or if the sequence contains a cycle \((a_k,\ldots,a_{m+k})\) where \(a_k = a_{k+m}\). My implementation of the length in lisp is as follows:

(defun run (n p &optional (m 0) (tail nil))
   (let ((res (g n p)))
      (if (or (= n 1) (member res tail))
         m
         (run res p (1+ m) (cons res tail)))))
RUN

I’ll show you several plots: for \(p=2\) (the original Collatz Conjecture case), and for \(p=3,5,7\) and one for a large \(p\) where \(p=103\).