Collatz Lengths (Continued)
I was looking at the following function \(f\colon\mathbb{N}\to\mathbb{N}\) defined as \[ f(n) = \begin{cases} 1 & \text{ if } n = 1\\ \frac{n}{2} & \text{ if $n$ is even}\\ \frac{3n+1}{2} & \text{ otherwise} \end{cases} \] and the recursive function \[ \ell(n) = \begin{cases} 0 & \text{ if } n = 1\\ 1 + \ell(f(n)) & \text{ otherwise } \end{cases} \] I am specifically interested in \(\ell(n)/\log_2(n)\).
Yesterday, I made a mistake in typing in \(f(n)\) and instead I defined \[ g(n) = \begin{cases} 1 & \text{ if } n = 1,3\\ \frac{n}{2} & \text{ if $n$ is even}\\ \frac{3(n+1)}{2} & \text{ otherwise} \end{cases} \] and I didn’t notice the mistake until later. If you have experimented with Collatz lengths you should know that it is a rather interesting accident that the recursive length terminates. So, having found another function whose termination behavior is similar to the original \(f(n)\) is nice.
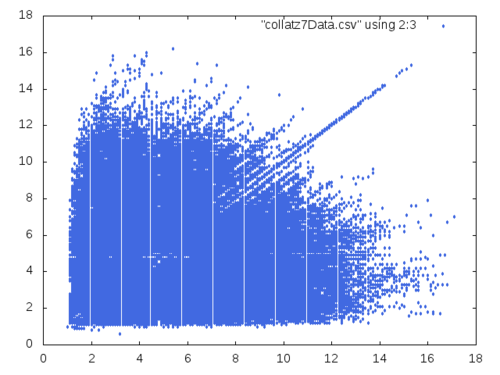
This gave me an idea: what if I plotted the lengths of sequences coming from \(f(n)\) and \(g(n)\) against each other would I see that the convergence behaviors of the recursive lengths are similar.
Code
First I will need our functions:
(defun f (n)
(cond ((= n 1) 1)
((evenp n) (/ n 2))
(t (/ (1+ (* 3 n)) 2))))
F
(defun g (n)
(cond ((< n 4) 1)
((evenp n) (/ n 2))
(t (* (/ 3 2) (1+ n)))))
GThen an iterator:
(defun iterate (fn n &optional (m 0))
(if (= n 1)
m
(iterate fn (funcall fn n) (1+ m))))
ITERATENext, the data on lengths:
(let ((n (expt 2 22))
(filename "collatz7Data.csv"))
(with-open-file (out filename
:direction :output
:if-exists :supersede
:if-does-not-exist :create)
(loop for i from 2 to n
do (let ((x (log i 2)))
(format out "~d ~4,1f ~4,1f~%"
i
(/ (iterate #'f i) x)
(/ (iterate #'g i) x))))))
NIL