An Implementation of Ford-Fulkerson Algorithm in Common Lisp

Description of the problem

Given a network where edges have predetermined capacities, our task is to determine the maximum possible flow between any two vertices in the network.

One possible solution is to use Ford-Fulkerson Algorithm. Today, I am going to implement Ford-Fulkerson in lisp.

Flow networks

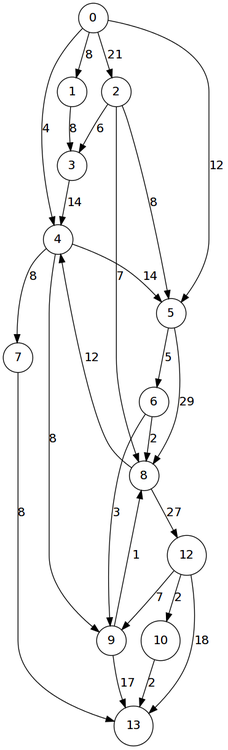
I am going to represent the graphs as pairs of vertices and a number representing the capacity in that particular direction. For example

(defvar G '(((0 1) . 3) ((1 2) . 1) ((1 3) . 1) ((2 4) . 2) 
            ((3 4) . 1) ((4 5) . 0) ((3 5) . 3) ((2 5) . 2) 
            ((5 6) . 1))) 

G

represents

Finding a path

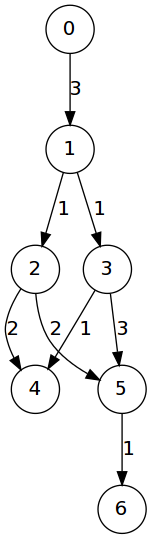
In order to implement the algorithm we are going to need find paths from the source to the sink. The function below will find such a path using a depth-first search.

(defun find-a-route (x y G &optional (past (list x)))
   (let* ((res nil)
          (neigh (dolist (i G (reverse res))
                    (if (and (> (cdr i) 0) (= x (caar i)))
                        (push (cadar i) res))))
          (next (set-difference neigh past)))
      (cond ((null next) nil)
            ((member y next) (reverse (push y past)))
            (t (some (lambda (i) (find-a-route i y G (cons i past))) next)))))

FIND-A-ROUTE

Augmented flow

Next, we need to find the maximum flow which is the minimum capacity on the path

(defun max-flow (path capacity)
   (let ((res (mapcar (lambda (x y) (cdr (assoc (list x y) capacity :test #'equal)))
                      path 
                      (cdr path))))
      (and res (apply #'min res))))

MAX-FLOW

The Ford-Fulkerson algorithm implemented

And finally here is an implementation of the Ford-Fulkerson maximum flow algorithm. Along each augmented path, we increase the flow and decrease the capacity. If there was a flow in the reverse direction, we also decrease that too, and on top of that, on the capacity network we add a reverse flow on such edges.

(defun ford-fulkerson (a b network)
   (let ((capacity (copy-list network))
         (flow (mapcar (lambda (x) (cons (car x) 0)) network)))
      (labels ((modify (edge net val)
                  (incf (cdr (assoc edge net :test #'equal)) val))
               (augment (path)
                  (let ((m (max-flow path capacity)))
                     (dolist (edge (mapcar #'list path (cdr path)))
                        (if (assoc edge flow :test #'equal)
                           (progn (modify edge flow m)
                                  (modify edge capacity (- m)))
                           (progn (modify (reverse edge) flow (- m))
                                  (if (assoc edge capacity)
                                      (modify edge capacity m)
                                      (push (cons edge m) capacity))))))))
         (do ((path (find-a-route a b capacity) (find-a-route a b capacity)))
             ((null path) flow)
           (augment path)))))

FORD-FULKERSON

Some tests

To test the algorithm I am going to need a random flow network. The following function will give us such a random flow network.

(defun random-graph (n m k)
  (remove-duplicates
     (loop for i from 0 to n append
         (loop repeat m collect
             (if (zerop (random 8))
                 (cons (list (+ i 1 (random m)) i) (1+ (random k)))
                 (cons (list i (+ i 1 (random m))) (1+ (random k))))))
  :test (lambda (x y) (or (equal (car x) (car y))
                          (equal (reverse (car x)) (car y))))))

RANDOM-GRAPH

So, here is a random flow network:

(defvar a-random-flow (random-graph 12 6 30))

A-RANDOM-FLOW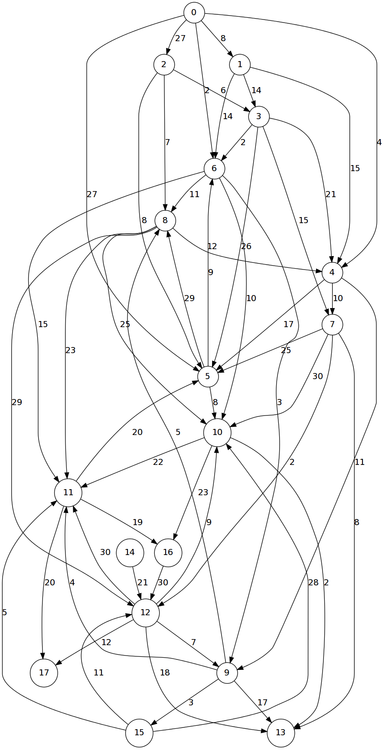

Let us find some random paths between points:

(find-a-route 0 13 a-random-flow)

(0 2 5 8 12 13)

Let us see if we get the right maximum flow:

(max-flow (find-a-route 0 13 a-random-flow) a-random-flow)

8

Let us test on our small network we defined at the very beginning:

And, now on the large random network I defined above:

(defvar flow (ford-fulkerson 0 13 a-random-flow))

FLOW