Tropic Calculation of Cheapest Paths

The Tropic Semi-Ring

There is this thing called the tropic semi-ring which is the set of non-negative real numbers together with the binary operations + and max. Notice that \[ a + \max(b,c) = \max(a,b) + \max(a,c) \] This means the triple \((\[0,\infty),\max,+)\) behaves similarly in terms of algebraic operations with the triple \((\[0,\infty),+,\cdot)\), but there are some drastic differences as well. For example, the unit for both operations is 0 in the tropic case, which is not true for the ordinary ring of real numbers.

One can also replace \(\max\) with \(\min\). In that case \(\min\) will cease to have a unit. As a matter of fact, in the discussion below I would prefer that I use \(\min\).

Matrices Over the Tropic Semi-Ring

Of course, one can define matrices over the tropic semi-ring. The matrix multiplication has to be modified as follows: if \(A = (a_{ij})\) and \(B = (b_{ij})\) are two compatible tropic matrices, then their product \(C = A\cdot B\) has the entries defined as \[ c_{ij} = \min_{k} (a_{ik} + b_{kj}) \] as expected.

Cheapest Path Calculation

Assume now that we have a matrix \(A = (a_{ij})\) of positive entries coming from a directed graph with positive weights. We set \(a_{ij}\) to \(\infty\) (or a very large number if you are going to be persnickety) if the nodes \(i\) and \(j\) are not connected via an edge in that direction. One can think of \(A\) as representing the price of direct connections. Now, the tropic product \(A\cdot A\) will give us the prices of 2-step cheapest connection, and by the similar token, \(A^n\) will give us the prices of n-step cheapest connections.

If the number of vertices is \(m\), the any cheapest path between any two vertices can not be longer than \(m-1\). This means we need the matrices \[ A, A^2,\ldots, A^{m-1}\] and no more. Since each product is of \(O(m^3)\), the time complexity of getting the sequence above is \(O(m^4)\).

An implementation

First, I am going to need a utility function that returns a specific row, or a column, of a matrix

(defun array-slice (arr i dir)
  (let ((n (elt (array-dimensions arr) (- 1 dir))))
    (if (zerop dir)
       (loop for j from 0 below n collect
            (aref arr i j))
       (loop for j from 0 below n collect
            (aref arr j i)))))

ARRAY-SLICE

Next, is my implementation of the tropic matrix multiplication. As a matter of fact, the function calculates the entry-wise minimums of \(A\) and \(A\cdot B\), which we need.

(defun tropic-mult (a b)
  (let ((n (array-dimensions a))
        (m (array-dimensions b)))
    (make-array (list (elt n 0) (elt m 1))
        :initial-contents 
        (loop for i from 0 below (elt n 0) collect
           (loop for j from 0 below (elt m 1) collect
              (reduce #'min
                      (cons (aref a i j) 
                            (mapcar #'+ 
                                    (array-slice a i 0) 
                                    (array-slice b j 1)))))))))

TROPIC-MULT

And finally,

(defun cheapest-routes (arr)
  (let ((n (array-dimension arr 0)))
    (do ((temp arr (tropic-mult temp arr))
         (i 0 (1+ i)))
        ((= i n) temp))))

CHEAPEST-ROUTES

I will test the code on a random network. The weight of non-existent edges are set to \(2^{10}\).

(defun random-net (n m)
  (let ((res (make-array (list n n) :initial-element 0)))
    (loop for i from 0 below (1- n) do
       (loop for j from (1+ i) below n do
          (let ((x (if (zerop (random 2))
                      (1+ (random m))
                      (expt 2 10))))
             (setf (aref res i j) x)
             (setf (aref res j i) x)))
       finally (return res))))

RANDOM-NET

(defvar network (random-net 8 20))

NETWORK

#2A((0 13 1024 1024 1024 12 1024 1024)
    (13 0 17 1024 2 1024 1024 1024)
    (1024 17 0 19 14 1024 15 1024)
    (1024 1024 19 0 1024 1024 1024 13)
    (1024 2 14 1024 0 16 6 14)
    (12 1024 1024 1024 16 0 7 14)
    (1024 1024 15 1024 6 7 0 15)
    (1024 1024 1024 13 14 14 15 0))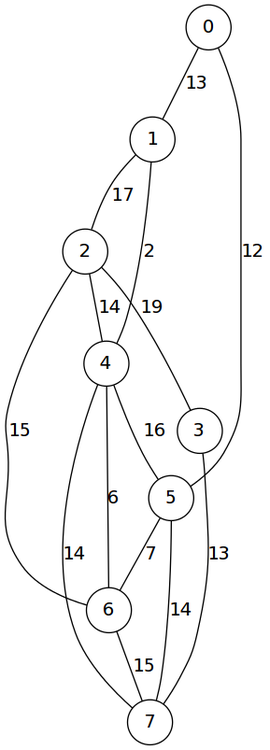

And the graph for the cheapest routes:

(cheapest-routes network)

#2A((0 13 29 39 15 12 19 26)
    (13 0 16 29 2 15 8 16)
    (29 16 0 19 14 22 15 28)
    (39 29 19 0 27 27 28 13)
    (15 2 14 27 0 13 6 14)
    (12 15 22 27 13 0 7 14)
    (19 8 15 28 6 7 0 15)
    (26 16 28 13 14 14 15 0))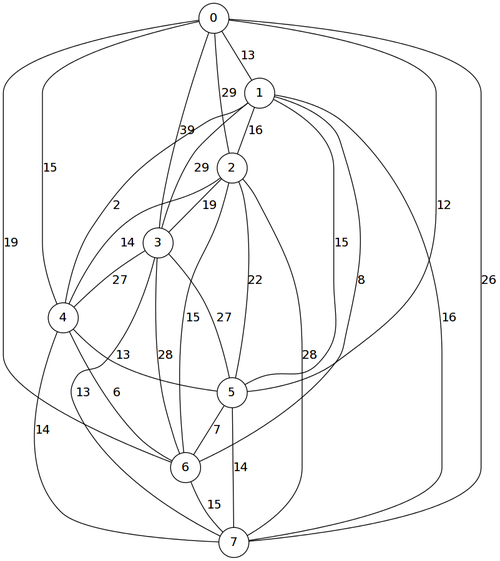

Why?

There other algorithms with \(O(n^2)\) complexity for dense graphs out there, for example Dijkstra’s Algorithm. But the algorithm I present above is extremely simple to implement, and it screams to be implemented concurrently on a multicore machine, or on a GPU.