Counting Spanning Trees of a Graph

Description of the Problem

Given a undirected graph \(G = (V,E)\), a spanning tree \(T\) of \(G\) is a connected subgraph of \(G\) which uses the full set of vertices but uses a minimal set of edges such that \(T\) has no cycles while still being connected. Today, we are going to count all spanning trees in a given graph.

Laplacian Matrix

In almost all of the graph algorithms I considered so far, I assumed my graphs were sparse: the number of edges were comparible to the number of vertices. Therefore, I almost invariably used a list of edges to represent a graph such as

(defvar G '((0 1) (1 2) (1 3) (2 4) (3 4)))

G

which represents the following graph

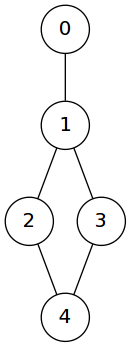
Of course there are other representations. One of them is the adjacency matrix which is a \(n\times n\) matrix which consists of 0’s and 1’s and defined as \[ a_{ij} = \begin{cases} 1 & \text{ if there is an edge between $i$ and $j$ }\\ 0 & \text{ otherwise } \end{cases} \] and yet another one is the Laplacian of a graph which is also an \(n\times n\) matrix given by \[ a_{ij} = \begin{cases} \deg(i) & \text{ if } i=j\\ -1 & \text{ if there is an edge between $i\neq j$ }\\ 0 & \text{ otherwise } \end{cases} \]

Kirchoff’s Theorem states that the determinant of any minor of the Laplacian will give us \(n\) times the number of spanning trees of \(G\).

Code

The following function returns the Laplacian matrix of a given graph represented as a list of edges. We assume edges are represented by lists of vertices of size 2, and that the vertices are numbered starting from 0.

(defun laplacian (G)
   (let* ((n (1+ (apply #'max (loop for x in G append x))))
          (m (make-array 
               (list n n) 
               :initial-element 0)))
     (loop for edge in G do
        (destructuring-bind 
             (a b) edge
          (incf (aref m a a))
          (incf (aref m b b))
          (decf (aref m a b))
          (decf (aref m b a))))
     m))

LAPLACIAN

Let us test:

(laplacian G)

#2A((1 -1 0 0 0) (-1 3 -1 -1 0) (0 -1 2 0 -1) (0 -1 0 2 -1) (0 0 -1 -1 2))

For the number of spanning trees, we will need to compute the determinant of any minor. In the following, I will delete the first row and the column.

(defun number-of-spanning-trees (G)
   (let* ((m (laplacian G))
          (n (array-dimension m 0))
          (x (grid:subgrid m (list (1- n) (1- n)) '(0 0))))
      (round (lla:det x))))

NUMBER-OF-SPANNING-TREES

(number-of-spanning-trees G)

4

Now, let us test something larger

(defvar H
   (remove-duplicates 
      (loop repeat 100 collect 
          (let* ((a (random 12))
                 (b (+ 1 a (random 9))))
             (list a b)))
      :test #'equal))
H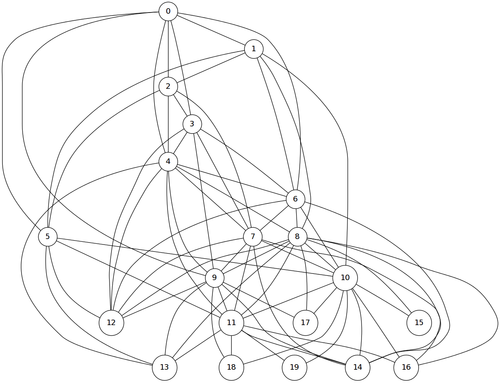

and the number of spanning trees for this graph is

(number-of-spanning-trees H)

51292592574547