Hashes and Entropy

Description of the problem

Today, I would like to investigate relative entropy change (before and after) in hashing. In others words, if I have a bag of words which have an initial entropy, after I hash these words what happens to the entropy of the resulting words?

Code

First, I need a random vector of 8-bit vectors:

(defun random-vector (n)
   (coerce (loop repeat n collect (random 256)) '(vector (unsigned-byte 8))))

RANDOM-VECTOR

But, I don’t need single individual words but sets of words since I need to calculate entropy:

(defun random-collection (n m)
   (loop repeat n collect (random-vector (+ 10 (random m)))))

RANDOM-COLLECTION

Now, the entropy function

(defun entropy (collection)
   (let ((result (make-array 256 :initial-element 0))
         (entrop 0.0d0)
         (N 0))
     (dolist (i (loop for x in collection append (coerce x 'list)))
        (incf (aref result i)))
     (setf N (reduce #'+ result))
     (- (log N 2) 
        (/ (reduce #'+ (map 'list (lambda (x) (if (> x 0) (* x (log x 2)) 0)) result)) 
           N))))

ENTROPY

For hashing I will use the ironclad crypto library. I will define several hash functions where each return a vector of 8-bit bytes.

(require :ironclad)

(SB-ROTATE-BYTE IRONCLAD)

(let ((hasher (ironclad:make-digest :md5)))
   (defun md5-digest (x)
      (ironclad:digest-sequence hasher x)))

MD5-DIGEST

(let ((hasher (ironclad:make-digest :sha1)))
   (defun sha1-digest (x)
      (ironclad:digest-sequence hasher x)))

SHA1-DIGEST

(let ((hasher (ironclad:make-digest :sha224)))
   (defun sha224-digest (x)
      (ironclad:digest-sequence hasher x)))

SHA224-DIGEST

The experiment

First, I need to write a function which will perform the numerical experiments:

(defun experiment (hashfn rep batch len filename)
   (with-open-file (data (concatenate 'string filename ".csv")
                         :direction :output
                         :if-exists :overwrite
                         :if-does-not-exist :create)
      (loop repeat rep do
         (let* ((N (+ 5 (random batch)))
                (M (+ 5 (random len)))
                (clear (random-collection N M))
                (hashed (mapcar hashfn clear)))
            (format data "~4,2f ~4,2f~%" (entropy clear) (entropy hashed))))))

EXPERIMENT

Next, let me see what happens with the MD5 hash:

(experiment #'md5-digest 1000 100 10 "hash2-data-md5")

NIL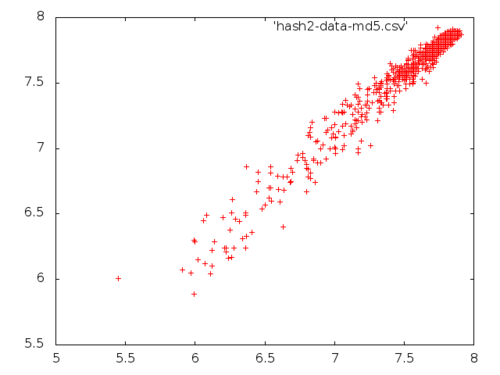

Now, with the SHA1 hash:

(experiment #'sha1-digest 1000 100 10 "hash2-data-sha1")

NIL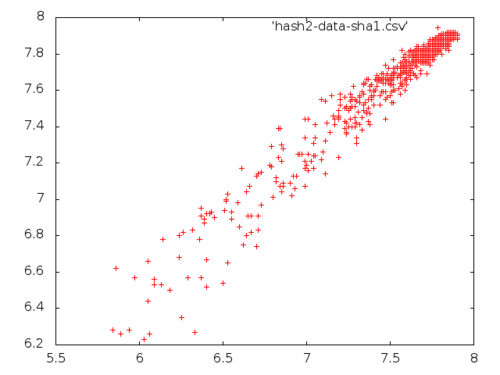

And, finally with SHA224 hash:

(experiment #'sha224-digest 1000 100 10 "hash2-data-sha224")

NIL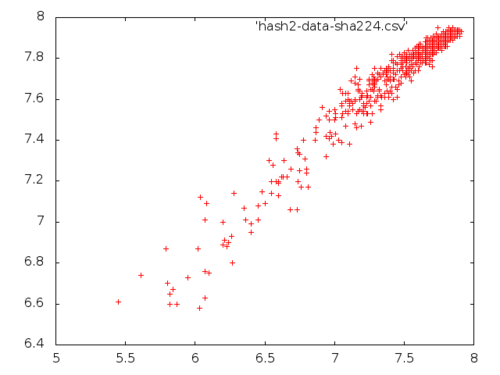

Analysis

The result is not surprising: hashing isn’t supposed to add or take away any entropy since we expect the hash to be collision-free. Mathematically speaking, we ask the hash function to be one-to-one in practice. Theoretically speaking, this is impossible, hence the adjective in practice. In any case, this was an interesting experiment to see if there is any weaknesses in the SHA1, SHA224 or MD5 hashing.

There is something interesting: There is a slight bent in the SHA224 graph above: it looks like it is sub-linear. This could be an artifact of the small sample size, and definitely worth investigating in the future.