A Zipf's Law Simulation

Problem description

Recently, I saw a nice algorithm by Vincent Granville that simulates samples obeying Zipf’s Law using a nice physical process. But I had to play with the parameters of the simulation a bit.

The algorithm

I will copy the description of the algorithm (with small changes) from Vincent:

1. Each particle is assigned a unique bin ID between 1 and \(N\). Each particle represents a cluster with one element (the particle),and the bin ID is its cluster ID.

2. Iteration: repeat \(r\) times:

3. 1. Randomly select two integers i and j between 1 and current number of clusters.
   2. If size of cluster i and cluster j are similar, merge these clusters with probability \(0<u<1\), Otherwise, merge these clusters with probability \(0<v<1\)
   3. Update cluster list

An implementation in lisp

The implementation was pretty straightforward.

Start with a comparison function that compares the sizes of two clusters. The following function is what I thought to be appropriate, but of course, you may change it to suit your needs.

(defun comp (a b &optional (eps 1d-1))
   (< (abs (- 5d-1 (/ a (+ a b)))) eps))

Now, the main function. The function takes the following parameters:

1. num: The size of the population.
2. rep: The number of times the simulation runs.
3. u: The probability that two similar clusters will merge.
4. v: The probability that two non-similar clusters will merge.

 (defun zipf-simulate (num rep u v)
    (let ((bag (loop for i from 0 below num collect (list i))))
      (loop while (and (cdr bag) (> rep 0)) do
         (let* ((m (length bag))
                (i (random m))
                (j (do ((k (random m) (random m))) ((not (= i k)) k)))
                (a (nth i bag))
                (b (nth j bag))
                (thrsh (if (comp (length a) (length b))
                          u
                          v)))
            (if (< (random 1.0d0) thrsh)
              (progn
                (nconc (nth i bag) b)
                (setf bag (delete b bag :test #‘equal))))
            (decf rep)))
      (sort (mapcar #'length bag) #’>)))

I ran the simulation with the parameters num=2000, rep=8000, u=0.8 and v=0.001 and the results were:

1048
513
256
128
32
16
4
2
1

The numbers decrease exponentially which is expected with such a small \(v\) parameter. Think of the extreme case of\(u=1.0\) (probability that two similar clusters will merge) and \(v=0.0\) (probability that two non-similar clusters will merge.) Then from an initial cluster of size \(N\) one gets sizes distributed exactly as the binary expansion of \(N\) which is quite interesting.

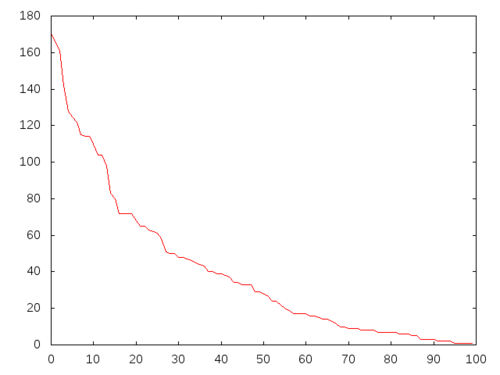
When I ran the simulation with the parameters (num=4095, rep=7600, u=0.8 and v=0.3) chosen along the lines Vincent suggested, I got something which is closer to what he expected.

And here are another implementation in (non-idiomatic) clojure in case common lisp is too archaic for you:

(defn zipf [n rep u v]
   (let [rnd (java.util.Random.)
         mycom (fn [a b] 
                  (if (< (Math/abs (- (double 0.5) (double (/ a (+ a b))))) 0.01)
                    (double u)
                    (double v)))]
     (loop [bag (map list (range n))
            cou rep]
       (if (or (zero? cou) (< (count bag) 2))
          (sort (map count bag))
          (let* [m (count bag)
                 i (.nextInt rnd m)
                 j (loop [j (.nextInt rnd m)] (if (not (= i j)) j (recur (.nextInt rnd m))))
                 a (nth bag i)
                 b (nth bag j)]
            (if (< (.nextFloat rnd) (mycom (count a) (count b)))
              (recur (cons (concat a b) (remove #{a b} bag)) (dec cou))
              (recur bag (dec cou))))))))