Information content of n-grams

Description of the problem

In a previous post I investigated the way the entropy increases as one increases the length of n-grams in genomic data. I had two questions after I completed that post:

1. Does the rate of change in entropy depend on the size of the sample?

2. How different is the rate of change from a completely random data.

The effect of the sample size

The following function reads the file and randomly samples at a rate supplied to the function.

(defun get-ngrams (file len rate)
   (with-open-file (in file :direction :input)
      (labels ((getline ()
                    (remove-if-not 
                       (lambda (x) (or (char= x #\a)
                                       (char= x #\t)
                                       (char= x #\g)
                                       (char= x #\c)))
                       (read-line in nil))))
         (let ((result (make-hash-table :test 'equal)))
            (do ((buffer 
                   (getline)
                   (if (<= (length buffer) len)
                      (concatenate 'string (subseq buffer 1) (getline))
                      (subseq buffer 1))))
                ((< (length buffer) len) result)
                (let ((key (subseq buffer 0 len)))
                   (if (< (random 1.0) rate) 
                      (setf (gethash key result) 
                            (1+ (gethash key result 0))))))))))

GET-NGRAMS

And the following code calculates the information content of the sampled data.

(defun entropy (data)
   (let ((res 0.0d0)
         (n 0))
     (maphash (lambda (x y)
                 (incf res (if (> y 0) (* y (log y 2.0d0)) 0))
                 (incf n y))
              data)
     (- (log n 2.0d0) (/ res n))))

ENTROPY

And finally the code that performs the analysis.

(defun analyze (filename len rate)
   (let ((result (loop for i from 1 to len collect
                     (entropy (get-ngrams filename i rate)))))
      (mapcar '- result (cdr result))))

ANALYZE

I will perform the analysis with sampling rates of 25%, 50% and 100%.

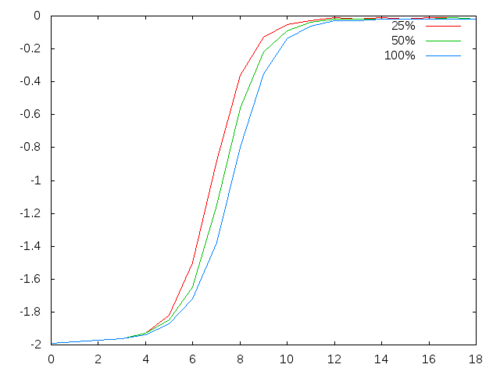
As the graph suggests, the phase transition happens at the same spot regardless of the sampling rate.

The comparison between the random data and genome data

For this part of the post I will write a function which will generate uniformly random sequences of letters “a”, “t”, “g” and “c”.

(defun random-ngrams (len rep)
   (let ((result (make-hash-table :test 'equal)))
      (labels ((getline () 
                 (coerce (loop repeat 100 collect (elt "atgc" (random 4))) 'string)))
         (do ((buffer (getline)
                      (if (<= (length buffer) len)
                         (concatenate 'string (subseq buffer 1) (getline))
                         (subseq buffer 1)))
              (i 0 (1+ i)))
             ((> i rep) result)
             (let ((key (subseq buffer 0 len)))
                (setf (gethash key result) 
                      (1+ (gethash key result 0))))))))

RANDOM-NGRAMS

Now, I will get the entropy for n-grams from \(n=1\) to \(n=20\) as did before and since the genome data contains \(4.6\times 10^6\) characters I will create a uniformly random data in equal size

(let* ((gene (analyze "../data/gene.txt" 20 1.0))
       (temp (loop for i from 1 to 20 collect 
                 (entropy (random-ngrams i 47538))))
       (rand (mapcar '- temp (cdr temp))))
  (with-open-file (out "information-output2.csv"
                       :direction :output
                       :if-exists :supersede
                       :if-does-not-exist :create)
     (mapcar (lambda (x y) (format out "~4,2f, ~4,2f~%" x y)) gene rand)))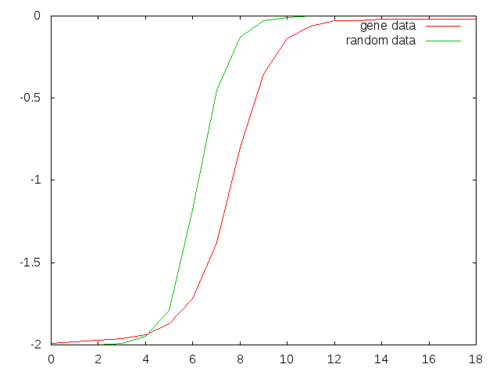

Phase transition occurs in the random data earlier and ends earlier than the genome data suggesting the entropy increases slower than the random data. Moreover, even though in the random data when n=10 the n-grams achieve information saturation (no new information can be obtained by increasing the lengths of n-grams) while the same maturation is achieved in the genome data when n=12.