Optimal length of n-grams
Description of the problem
The other day I was looking at a problem of determining how long a string one needs to use to identify a large text. As we increase the length of the substring, the chances of an accidental match reduces. However, there will be a sweet spot: after a point increasing the length of the substring will not give us an additional information. Today, I will try to figure out this breaking-point.
An experiment
For todays experiment I will use a sample from genome data GenBank and I will compare the results with “Huckleberry Finn” by Twain. The gene data is a collection of sequences with metadata. In order to get to the genome data, I needed to strip out the metadata and get to the sequence data. Luckily that data is stored within two markers in between “ORIGIN” and “//”. You can whip up a simple perl script (I show my age, aren’t I :) to do that.
I will load the data, and then create the frequency table of n-grams and then compute the entropy of this resulting table. Changes in the entropy will give us the information we need. The following lisp function creates a frequency table for a given length n-gram.
(defun get-ngrams (file len getline)
(let* ((result (make-hash-table :test 'equal)))
(with-open-file (in file :direction :input)
(do ((buffer
(funcall getline in)
(if (< (length buffer) (1+ len))
(concatenate 'string (subseq buffer 1) (funcall getline in))
(subseq buffer 1))))
((< (length buffer) len) result)
(let ((key (subseq buffer 0 len)))
(setf (gethash key result)
(1+ (gethash key result 0))))))))
GET-NGRAMSAnd then we calculate the entropy in a modified form. See here on why I do that.
(defun temperature (hash)
(let ((result 0.0d0))
(maphash
(lambda (x y) (incf result (* y 1.0d0 (log y))))
hash)
result))
TEMPERATUREThen, since I am looking for a phase transition, I need to look at the first derivative of the results:
(defun diff (sequence)
(let (result)
(do* ((x sequence (cdr x)))
((null (cadr x)) (nreverse result))
(push (- (cadr x) (car x)) result))))
DIFFNow, let us see what is going on:
(defun get-line-genome (stream)
(remove-if-not
(lambda (x) (or (char= x #\a)
(char= x #\t)
(char= x #\g)
(char= x #\c)))
(read-line stream nil)))
GET-LINE-GENOME
(with-open-file (out "ngrams-out1.csv"
:direction :output
:if-exists :supersede
:if-does-not-exist :create)
(let ((temps (diff (loop for i from 1 to 17
collect (temperature
(get-ngrams
"../data/gbbct112-processed.seq"
i
'get-line-genome))))))
(dotimes (i (length temps)) (format out "~d ~12,8f~%" (1+ i) (elt temps i)))))
NIL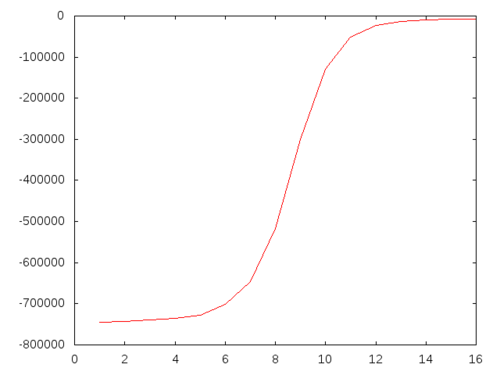
From this graph we see that increasing the length of n-grams do not yield much on the interval 1 to 5. There is a phase transition at n=6. Any increase result in drastic changes on the interval 6 to 10. Then there is another phase transition at n=11. This suggests that I should pay attention n-grams of length 6 and 11.
Now, I will repeat the test with Huckleberry Finn. For that I will need to modify the function which reads the lines from the input file.
(defun get-line-text (stream)
(remove-if-not
(lambda (x) (or (char= x #\Space)
(and (char>= x #\a)
(char<= x #\z))))
(read-line stream nil)))
GET-LINE-TEXT
(with-open-file (out "ngrams-out2.csv"
:direction :output
:if-exists :supersede
:if-does-not-exist :create)
(let ((temps (diff (loop for i from 1 to 40
collect (temperature
(get-ngrams
"../data/twain-huckleberry-finn.txt"
i
'get-line-text))))))
(dotimes (i (length temps)) (format out "~d ~12,8f~%" (1+ i) (elt temps i)))))
NIL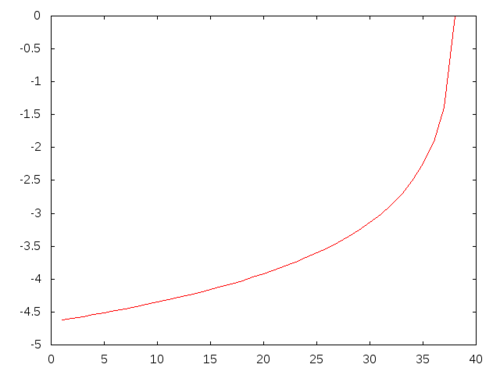
There is no phase transition in this example. The longer the n-grams the better the result. And since the entropy becomes the maximum at n=38 I must choose n=38 or higher.