Tree Isomorphism

Description of the problem

Deciding whether two graphs $(E,V)$ and $(E',V')$ are isomorphic is a difficult problem. Best known algorithms are of exponential complexity. However, for trees the situation is much simpler. Today, I will describe and implement a simple algorithm to decide if two trees are isomorphic. I basically followed Eric Thierry’s excellent notes on the subject. (All errors are mine, of course.) Thierry claims the algorithm is of linear complexity following Valiente, but because of the sorting part involved in the algorithm, it seems more like $\mathcal{O}(n\log(n))$.

The Algorithm and Its Correctness

For us, a (labeled) graph is a pair $(E,V)$ such that $V$ is a finite subset of $\mathbb{N}$ of type ${0,\ldots,n-1}$, and $E$ is a collection of 2-element subsets of $V$. A tree is a graph in which every vertex $m\in V$ is connected to $0\in V$ via a unique path.

Let $\mathcal{T}$ be the set of all rooted trees (the vertex 0 is defined to be the root) as we defined above. We want to construct a function $\Upsilon$ from the set of trees into the set of finite sequences of natural numbers such that $\Upsilon(T_1) = \Upsilon(T_2)$ if and only if $T_1$ and $T_2$ are isomorphic. I will define the function recursively as follows:

Define $\Upsilon(\bullet) = (0)$.
Let $T$ be a tree and let $T_1,\ldots,T_m$ be the set of subtrees connected to the root. Assume we calculated $\Upsilon(T_i)$ for $i=1,\ldots,m$. Sort them as $\Upsilon(T_{i_1}) \preceq \cdots \preceq \Upsilon(T_{i_m})$ using the lexicographical ordering on the set of all finite sequences in $\mathbb{N}$. Now, define \[ \Upsilon(T) = (m, \Upsilon(T_{i_1}), \ldots, \Upsilon(T_{i_m}) ) \]

The function is well-defined for any tree $T$ as the notion of the subtrees connected to the root is a well-defined notion and we defined $\Upsilon(\bullet)$. What remains to be shown is that $\Upsilon(T_1)$ and $\Upsilon(T_2)$ are equal if and only if the trees are isomorphic.

One side of the implication is straightforward: if $T_1$ and $T_2$ are isomorphic then $\Upsilon(T_1)=\Upsilon(T_2)$. This is basically recursion/induction on the number of vertices in the tree.

For the converse, assume $\Upsilon(T_1) = \Upsilon(T_2)$. In that case, we have

The first terms of $\Upsilon(T_1)$ and $\Upsilon(T_2)$ are equal which means the number of subtrees connected to the root are the same for $T_1$ and $T_2$
The subtrees of $T_1$ and $T_2$ produce the same sequence of terms out of $\Upsilon$.

Then again using an induction/recursion argument on the number of vertices in a tree, we get the reverse implication.

An Implementation

We will describe trees using lisp lists. For example, the following list

(defvar tree-1 '(* * (* * *) (* *) (* (* * *))))

describes the following tree:

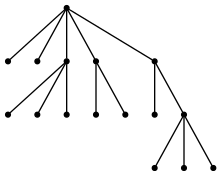
However, the tree above and the tree given by

(defvar tree-2 '(* * (* *) (* * *) (* (* * *))))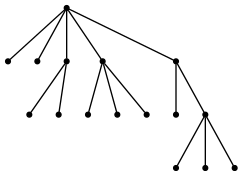

are isomorphic trees.

In order to implement the algorithm I described in the first section, I will need a lexicographical comparison function for sequences of integers:

(defun compare (a b)
  (cond ((and (atom a) (atom b)) (< a b))
        ((atom a) 't)
        ((atom b) nil)
        ((equal (car a) (car b)) (compare (cdr a) (cdr b)))
        (t (compare (car a) (car b)))))

Actually, compare does more than comparing lists of integers. I will leave it up to you to figure out why and how. Now, the function $\Upsilon$:

(defun upsilon (tree)
  (cond ((null tree) nil)
        ((atom tree) (list 0))
        (t (cons (length tree)
                 (reduce 'append (sort (mapcar 'upsilon tree) 
                                       'compare))))))

which implements the function which checks for isomorphism

(defun tree-isomorphic-p (tree1 tree2)
  (equal (upsilon tree1) (upsilon tree2)))

Let me test it on the trees I defined above:

(tree-isomorphic-p tree-1 tree-2)
T

and test on a pair which is not isomorphic:

(tree-isomorphic-p '((* *) ((* *) * (* *))) '(* * (* (*) (* *))))
NIL

Addendum

There is a short-cut for the solution I gave for the tree isomorphism problem: the function compare I defined above does define a total order on the set of trees. So, I can use it to transform trees into a canonical form. Once they are in canonical form, two trees are isomorphic if and only if they are are equal. It is that easy.

(defun compare-trees (a b)
  (cond ((and (atom a) (atom b)) 't)
        ((atom a) 't)
        ((atom b) nil)
        ((equal (car a) (car b)) (compare-trees (cdr a) (cdr b)))
        (t (compare-trees (car a) (car b)))))

(defun canonical-form (tree)
  (if (atom tree)
      tree
    (sort (mapcar 'canonical-form tree) 'compare-trees)))

CANONICAL-FORM

Let me test it:

(canonical-form '(* * (* * *) (* *) (* (* * *))))
(* * (* *) (* * *) (* (* * *)))


(canonical-form '(* * (* *) (* * *) (* (* * *))))
(* * (* *) (* * *) (* (* * *)))