Logistic Regression in lisp
Description of the problem
I was looking at the code I wrote for my Gradient Descent post and there is room for improvement. I will refactor the code, and add a new application: I will do Logistic Regression using Gradient Descent.
Ordinary least square regression revisited
Let me go over the setup: we have a finite dataset \(x^{(1)},\ldots,x^{(n)}\) of points coming from a \(m\)-dimensional vector space. For each of these points we have a numerical response variable \(y^{(i)}\) for \(i=1,\ldots,n\). We want to approximate \(y^{(i)}\) using \(x^{(i)}\) via a linear equation of the type \[ y^{(i)} = {\mathbf a}\cdot x^{(i)} + b \] In the ordinary least squares resgression we minimize the total error: \[ LSE({\mathbf a},b) = \frac{1}{2n}\sum_{i=1}^n \|y^{(i)}-{\mathbf a}\cdot x^{(i)}-b\|^2 \] over the parameters \({\mathbf a}\) and \(b\).
Logistic regression
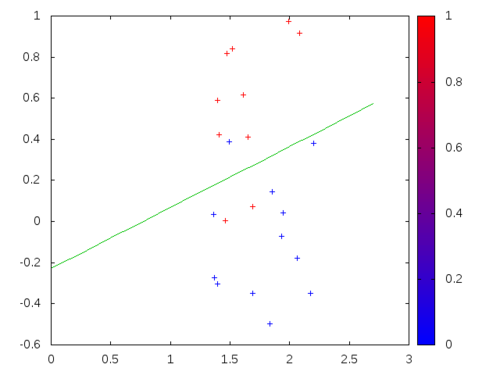
If the responses \(y^{(i)}\) are discrete, specifically if they take only two values (say 0 and 1), then we can use another statistical model called Logistic Regression. The biggest difference comes from the fact that this problem is not a regression problem, rather a classification problem. We must split the vector space (and therefore the dataset) into 2 halves so that datapoints with \(y^{(i)}=0\) and \(y^{(i)}=1\) lie on different sides.
Notice that \[ {\mathbf a}\cdot {\mathbf x} + b = 0\] is an equation of a hyper-plane and each side of the hyper-plane is determined by the sign of the auxiliary function \[ f({\mathbf x}) = {\mathbf a}\cdot {\mathbf x} + b \] Larger the norm \(\|f({\mathbf x})\|\) the more confident one has to be that \({\mathbf x}\) belongs to the correct side of the hyper-plane in question. At this stage, the Logistic Function \(\frac{1}{1+exp(-x)}\) comes to our rescue.
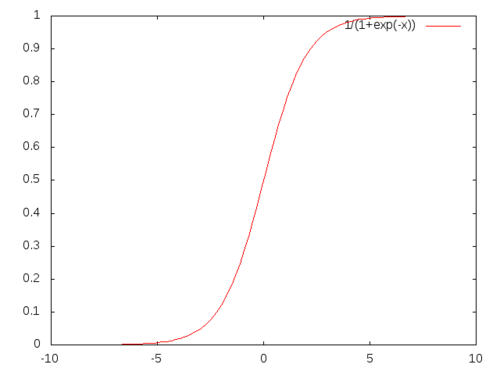
Let us say that the probability of a point \({\mathbb z}\) being on the positive side of the hyper-plane \({\mathbf a}\cdot {\mathbf x}+b=0\) is \[ \frac{1}{1+\exp(-{\mathbf a}\cdot {\mathbf z} - b)} \] Using this we can write a probability function \(p({\mathbf z},y)\) \[ p({\mathbf z},y) = \left(\frac{1}{1+\exp(-{\mathbf a}\cdot {\bf z} - b)}\right)^y \left(\frac{1}{1+\exp({\mathbf a}\cdot {\bf z} + b)}\right)^{1-y} \] which measures the probability of \({\bf z}\) being on the right side where \(y\) takes values 0 or 1. Then the probability that all of the points in our dataset being on the right side is \[ p(D) = \prod_{i=1}^n p(x^{(i)},y^{(i)}) \] and therefore we would like to maximize \(p(D)\) depending on the unknown parameters \({\mathbf a}\) and \(b\). Instead one can minimize the following function \[ LE({\mathbf a},b) = -\frac{1}{n}\sum_{i=1}^n y^{(i)}\log(1+\exp(-{\mathbf a}\cdot x^{(i)} - b)) + (1-y^{(i)})\log(1+\exp({\mathbf a}\cdot x^{(i)} + b)) \] which is just the natural logarithm of \(p(D)\). This is the part I am going to tackle with a new and slightly improved gradient descent.
The refactored code
Without further ado, here is the new refactored code.
(defun descent (fun x &key (error 1.0d-4)
(rate 1.0d-2)
(debug nil)
(max-steps 1000))
(labels
((make-step (y)
(loop for i from 0 below (length y) collect
(let ((ini (copy-seq y))
(ter (copy-seq y)))
(incf (aref ter i) error)
(decf (aref ini i) error)
(* (- (funcall fun ter)
(funcall fun ini))
(/ rate error 2)))))
(norm (y) (sqrt (reduce '+ (map 'list (lambda (i) (* i i)) y)))))
(do* ((y x (map 'vector '- y step))
(step (make-step y) (make-step y))
(n 1 (1+ n)))
((or (< (norm step) error) (>= n max-steps)) (values y n))
(if (and debug (zerop (mod n 100)))
(format t "~4D ~6,7F (~{~4,2F~^, ~})~%" n (norm step) (coerce y 'list))))))The two biggest differences are (1) I am using labels
instead of using defun for auxiliary code, and (2) the
derivative code is streamlined to be more efficient. In this form the
function descent is a standalone function. It doesn’t need
anything else. You can cut-and-paste it as is and start using it.
Least square regression re-revisited
I will re-implement the least square regression again to test the code.
(defun least-square-err (data)
(lambda (x)
(* (/ 1.0d0 (length data))
(loop for point in data sum
(let* ((N (1- (length point)))
(z (copy-seq point))
(y (aref point N)))
(setf (aref z N) 1)
(expt (- y (reduce '+ (map 'vector '* z x))) 2))))))
(defparameter my-data
(let ((a (- (random 4.0) 2.0))
(b (- (random 2.0) 1.0)))
(mapcar (lambda (x) (coerce (list x (+ b (* a x) (- (random 0.8) 0.4))) 'vector))
(loop for i from 1 to 30 collect (random 2.0)))))
(defparameter my-err (least-square-err my-data))
(defparameter theta (descent my-err #(1.0 -1.2)
:rate 9.0d-2
:error 1.0d-4
:max-steps 500
:debug nil))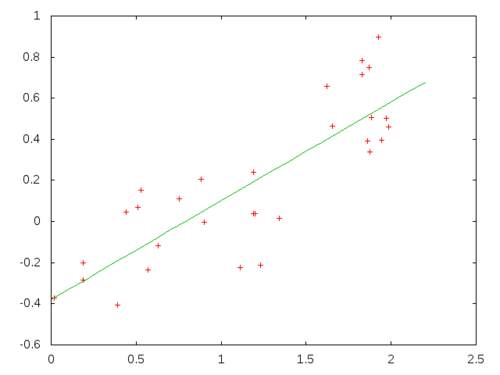
Logistic regression
Now, comes the implementation of the function we would like to minimize
(defun logistic-err (data)
(lambda (x)
(* (/ -1.0d0 (length data))
(loop for point in data sum
(let* ((y (copy-seq point))
(N (1- (length y)))
(b (aref y N))
res u)
(setf (aref y N) 1)
(setf res (reduce '+ (map 'vector '* x y)))
(setf u (/ 1.0d0 (+ 1.0d0 (exp res))))
(+ (* (log u) (- 1.0d0 b))
(* (log (- 1.0d0 u)) b)))))))As before, this function takes a dataset and then returns a function
that descent will try to minimize. Let me create an example
dataset to work on:
(defparameter my-data
(labels
((range (n) (loop for i from 0 to n collect i))
(here (n b)
(map 'vector (lambda (x) (if (< x n) (random 1.0) b)) (range n)))
(there (a b)
(map 'vector '+ (append a (list 0)) (here (length a) b))))
(union (loop repeat 12 collect (there '(1.3 -0.6) 0))
(loop repeat 10 collect (there '(1.1 0.0) 1)))))First we create our function which we would like to minimize, and
then we feed it to descent:
(defparameter my-err (logistic-err my-data))
(defparameter theta (descent my-err #(0.0 0.0 0.0)
:max-steps 2000
:error 1.0d-5
:rate 9.0d-2
:debug nil))Let us see the fitted data: