Cut points in a graph

Description

Let \(G = (V,E)\) be a finite undirected graph. A vertex \(v\in V\) is called a cut point, or an articulation if after we remove \(v\) and all edges that \(v\) belongs to, we get a disconnected graph. For the sake of completeness, a graph is connected if one can travel between any two vertices following a sequence of edges.

An algorithm

Here is a simple idea for an algorithm: let us remove \(v\) and all edges \(v\) belongs to and then take a vertex \(w\) from the remaining graph. Let me denote the remaining graph by \(G\setminus v\). Let \(U_0 = \{w\}\) and let us define \(U_{n+1}\) as the set of neighbors of the vertices in \(U_n\). Since \(G\) is a finite graph this procedure will create stabilize after some index. If \(G\setminus v\) is connected, the procedure will stabilize at \(V\setminus{v}\), otherwise we will get a smaller set.

 Algorithm CutPoint
   Input: a graph G and a vertex v
   Outut: TRUE if v is an articulation, FALSE otherwise
 Begin
   Let H be the graph G from which v is removed
     together with all edges containing v
   Let w be a vertex from H
   Let S be the one-vertex set {w}
   Let U to be the emptyset
   While S is not equal to U do
      Let U be S 
      For each x in U do
          Add all the neighbors of x to S
      End
   End
   If S is equal to V \ {v} then
      Return FALSE
   Else
      Return TRUE
   End
 End

An implementation

As before, I will use ordered pairs to denote edges and a lisp list of edges to denote a graph. Here is an example I will use throughout this text:

(defparameter G '((0 1) (1 2) (2 3) (2 4) (3 5) (4 5) (5 6) (5 7) (2 7)))
G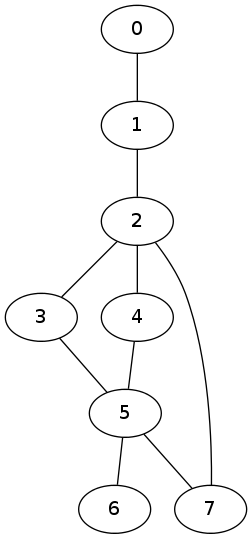

I will start by defining some utility functions. First, a function which returns the set vertices of a given graph:

(defun vertices (G)
   (remove-duplicates (loop for x in G append x)))
VERTICES

Let me test this function on G we defined above

(vertices G)
(0 1 3 4 6 5 2 7)

Here is a function which returns the list of neighbors of a vertex in a graph

(defun neighbors (v G) 
   (let ((H (copy-list G)))
       (vertices (delete-if (lambda (x) (not (member v x))) H))))

(neighbors 3 G)
(2 3 5)

Now, a function which will remove a vertex and all edges containing that vertex

(defun delete-vertex (v G)
   (let ((H (copy-list G)))
       (delete-if (lambda (x) (member v x)) H)))
DELETE-VERTEX

Let me test this on G again

(delete-vertex 4 G)
((0 1) (1 2) (2 3) (3 5) (5 6) (5 7) (2 7))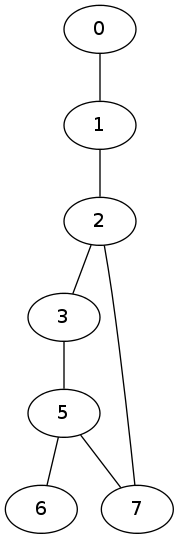

(delete-vertex 1 G)
((2 3) (2 4) (3 5) (4 5) (5 6) (5 7) (2 7))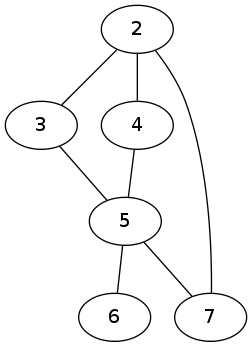

There is an obvious problem with the last example: since I do not keep the set of vertices as a seperate entity, if it happens that a vertex is left isolated without any edges it does not appear in the list of vertices. This can be amended by adding an artificial collection of loops on vertices

(setf G (append G (loop for i in (vertices G) collect (list i i))))
((0 1) (1 2) (2 3) (2 4) (3 5) (4 5) (5 6) (5 7) (2 7) (0 0) (1 1) (3 3)
 (4 4) (6 6) (5 5) (2 2) (7 7))

and now when we remove the vertex 1 we get

(delete-vertex 1 G)
((2 3) (2 4) (3 5) (4 5) (5 6) (5 7) (2 7) (0 0) (3 3) (4 4) (6 6) (5 5)
 (2 2) (7 7))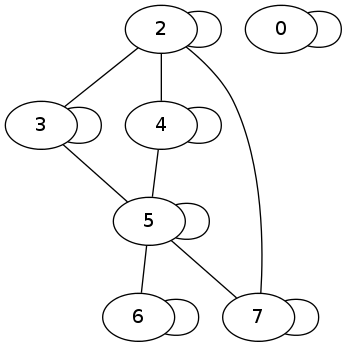

as we wanted. When I implement the main function I will have to add redundant loops, but for now let me remove these from my graph.

(delete-if (lambda (x) (equal (car x) (cadr x))) G)
((0 1) (1 2) (2 3) (2 4) (3 5) (4 5) (5 6) (5 7) (2 7))

Now, let me implement the main function:

(defun articulationp (v G)
   (let* ((VG (vertices G))
          (H (delete-vertex v G))
          (S (list (car (vertices H))))
          (H (append H (loop for i in VG collect (list i i))))
          (U nil))
     (loop while (not (equal S U)) do
          (setf U (copy-list S))
          (nconc S (loop for x in U append (neighbors x H)))
          (setf S (remove-duplicates S)))
     (not (equal (sort (cons v S) '<) 
                 (sort VG '<)))))
ARTICULATIONP

Let me test the function on few non-articulations. It should return NIL.

(articulationp 4 G)
NIL

(articulationp 0 G)
NIL

And now on an articulation point. It should return T.

(articulationp 1 G)
T