Experiments on Collatz Lengths (Continued)

Description of the problem

Today, I will continue on my experiments on Collatz sequences. Here is the setup: I have the following function \[ f(n) = \begin{cases} 1 & \text{ if } n=1\\ f(n/2) & \text{ if $n$ is even }\\ 3n+1 & \text{ otherwise} \end{cases} \] I am primarily interested in the behaviour of the recursive sequence \(a_{n+1} = f(a_n)\) for different initial values \(a_0\). The conjecture is that this sequence stabilizes at 1 for every initial value \(a_0\). One of the numbers I am interested in is the length of the recursive sequence before it hits 1. \[ len(a) = \min\{n\|\ a_n = 1 \text{ when } a_0 = a \} \] Now, I would like to add another function to the mix. Let me define a new function \[ \ell(n) = \begin{cases} \ell(n/2) & \text{ if $n$ is even }\\ 1+\lfloor \log_2(n) \rfloor & \text{ if $n$ is odd}\\ \end{cases} \] Notice that the fact that our recursive sequence stabilizes at 1 is equivalent to the fact that \(\ell(a_n)\) is eventually 1.

Today, I would like to look at the distribution of \(len(a)/\ell(a)\).

Implementation

First, I will need the base function.

(defun f(n)
   (cond ((equal n 1) 1)
         ((evenp n) (f (/ n 2)))
         (t (1+ (* 3 n)))))

Now, the \(\ell\) function

(defun ell (n)
   (cond ((equal n 1) 1)
         ((evenp n) (ell (/ n 2)))
         (t (1+ (floor (log n 2))))))

And finally an iterator implemented with a rudimentary memoization

(defparameter iter-table (make-hash-table :test 'equal))

(defun iter-lookup (n)
   (gethash n iter-table))

(defun iter-push (n val)
   (setf (gethash n iter-table) val))

(defun iter (n)
   (if (equal n 1)
       1
       (or (iter-lookup n)
           (iter-push n (1+ (iter (f n)))))))

Let me display the results between 1 and \(2^{22} = 4194304\). I used the following helper code to generate the sequence:

 (with-open-file (results "collatz4.csv"
                          :direction :output
                          :if-exists :supersede
                          :if-does-not-exist :create)

      (loop for i from 1 to (expt 2 22) do
            (format results "~A ~A~%" i (/ (len i) (ell i) 1.0))))

I passed the resulting file through gnuplot and got the following graph:

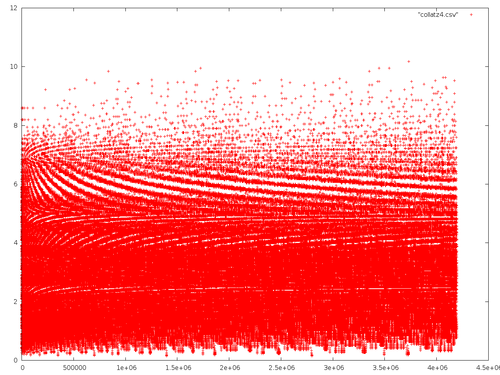
which is not very comprehensible. So, here is the first 30000 terms

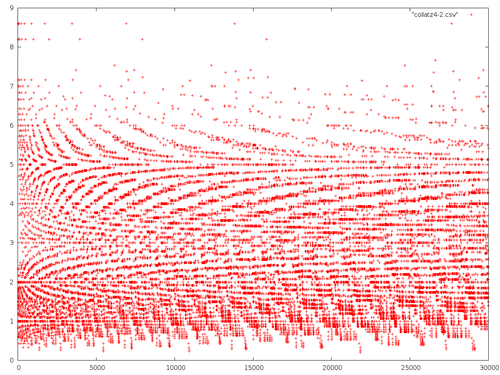
and the last 30000 terms

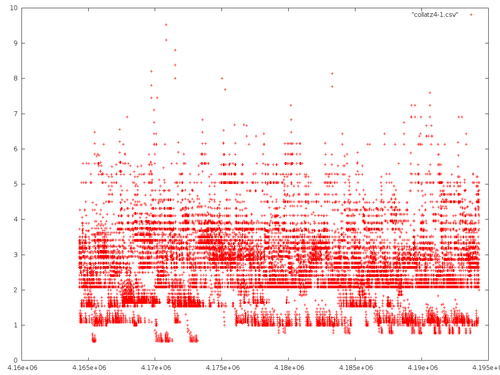
Another Implementation in Julia

I just realized I haven’t coded in Julia in a while. So, here is an implementation of the code above in julia.

function f(n)
  if n ==  1 then
     return 1
  elseif mod(n,2) ==  0 then
     return f(n/2)
  else
     return 3*n+1
  end
end


function iter(n)
  if n ==  1 then
     return 1
  else
     return 1+iter(f(n))
  end
end

function ell(n)
  if n ==  1 then
     return 1
  elseif mod(n,2) ==  0 then
     return ell(n/2)
  else
     return 1+floor(log(n)/log(2))
  end
end

A = [(i,iter(i)/ell(i)) for i in 1:4194304]

The julia code above took about 60 seconds to run on my dinky laptop with its Intel® Core™ i5-2430M CPU and 4Gb of RAM. The lisp code on sbcl took about 23 seconds on the same machine :) Ok, I am cheating of course since the lisp code cuts down the computation time using a basic memoization trick. But still, sbcl has been pleasantly surprising me with its superior performance in numerical calculations.