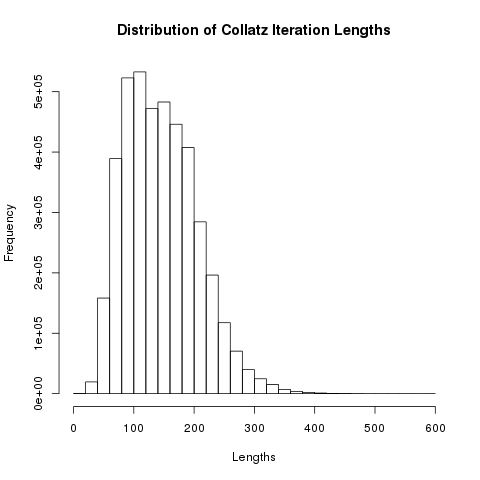
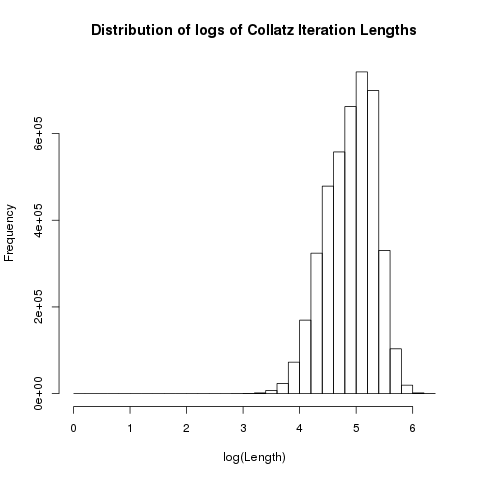
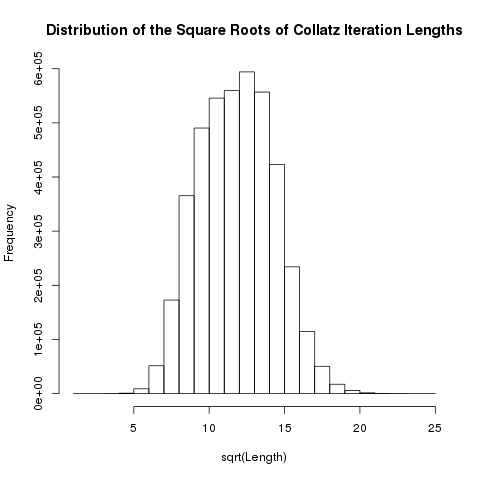
Distribution of Collatz Lengths

Desription of the problem

Consider the following function \[ f(n) = \begin{cases} \frac{n}{2} & \text{ if $n$ is even }\\ 3n + 1 & \text{ otherwise } \end{cases} \] and the recursive sequence \(a_{n+1} = f(a_n)\). It was conjectured that the sequence will produce \(1\) eventually for every initial value \(a_0\). Despite the very simple description, this turns out to be a notoriously difficult problem to solve.

Today, I will write a short lisp program to perform some numerical experiments on the problem. Also, I noticed that there there were no visualizations of the distribution of the lengths of the recursive sequences I defined above for different initial values.

Lisp code

I will start with the function:

(defun f(n) 
   (if (evenp n) 
      (/ n 2) 
      (1+ (* 3 n))))
F

and then another function which will iterate `f` until it hits 1

(defvar upper-limit (expt 2 22))

(defparameter iterate-table (make-hash-table :test 'equal))
(defun iterate-lookup (x) (gethash x iterate-table))
(defun iterate-push (x val) (setf (gethash x iterate-table) val))

(defun iterate(n)
    (if (= n 1) 
       0
       (or (iterate-lookup n)
           (let ((temp (1+ (iterate (f n)))))
               (if (< n upper-limit)
                  (iterate-push n temp)
                  temp)))))
ITERATE

Let me run the code:

(time (loop for n from 1 to upper-limit 
                do (iterate n)))

Evaluation took:
 4.724 seconds of real time
 4.716294 seconds of total run time (4.628289 user, 0.088005 system)
 [ Run times consist of 0.072 seconds GC time, and 4.645 seconds non-GC time. ]
 99.83% CPU
 11,310,793,128 processor cycles
 171,957,200 bytes consed

(with-open-file (results "collatz.csv" 
                         :direction :output
                         :if-exists :supersede
                         :if-does-not-exist :create)
                (maphash (lambda (x y) (format results "~A ~A~%" x y)) iterate-table))
NIL

And here is the distribution of the lengths of the Collatz sequences for all initial values between 1 and \(2^{22}\)