Path ideals

Description of the problem

Let \(G = (V,E)\) be a directed graph without loops and multiple edges. In other words \(V\) is a finite set and \(E\) is a subset of \(V\times V\) which does not contain elements of the form \((x,x)\) with \(x\in V\). I will also assume that \(G\) contains no oriented cycles and \(V\) is a subset of the set of natural numbers \(\mathbb{N}\) of the form \(\{0,1,\ldots,n\}\) and that edges in \(G\) are increasing. Increasing labelling is possible in cycle-free graphs because of topological sort.

In this context a path is a sequence of vertices \((v_0,\ldots,v_n)\) such that any two consecutive vertices are connected by an edge. Today, I will develop an algorithm and the accompanying lisp code which will give the set of all paths which contain specific paths as subpaths.

Some poset theory

You don’t need to read this section if you are only interested in the algorithm but my warped mathematician mind requires that I think about it.

Basics and few examples

A partially ordered set (a poset in short) is a pair \((P,\vdash)\) where \(P\) is a set and \(\vdash\) is a subset of the cartesian product \(P\times P\). Tradition dictates that instead of writing \((x,y)\in \vdash\), we write \(x\vdash y\). The subset \(\vdash\) must satisfy certain conditions:

• Reflexivity: for every \(x\in P\) we must have \(x\vdash x\)
• Anti-symmetricity: for every \(x,y\in P\), if \(x\vdash y\) and \(y\vdash x\) then \(x=y\)
• Transitivity: for every \(x,y,z\in P\), if \(x\vdash y\) and \(y\vdash z\) then \(x\vdash z\)

The set of natural numbers \(\mathbb{N}\) together with the ordinary order relation \(\leqslant\) is an example of a poset. Another good example is the set of English words and the lexicographical ordering + reflexivity. But, let me give you a non-example: let \(P\) be the set \(B=\{0,1\}\) and let \[ \prec\quad := B\times B = \{ (0,0), (0,1), (1,0), (1,1) \} \] The set \(\prec\) satisfies reflexivity and transitivity but doesn’t satisfy anti-symmetricity.

The relevant example

The relevant example for me is the set of all paths in a directed graph under the “subpath” relation. Let \(P(G)\) be the set of all paths in \(G\) and I will define \(\vdash \subseteq P(G)\times P(G)\) as follows: Let \(\alpha,\beta\in P(G)\). Assume \(\alpha=(a_0,a_1,\ldots,a_n)\) and \(\beta=(b_0,\ldots,b_m)\). I will write \(\alpha\vdash\beta\) if \(\alpha\) appears as a full segment of \(\beta\). That is, if there exists an index \(i\) such that \(b_{i+j} = a_j\) for any \(j=0,\ldots,n\). The fact that \(\vdash\) is reflexive and transitive is simple to see. Showing that \(\vdash\) is anti-symmetric requires that we consider the lengths of the paths involved: If \(\alpha\vdash \beta\) and \(\beta\vdash\alpha\) then the lengths of \(\alpha\) and \(\beta\) are equal, and since \(\alpha\) appers in \(\beta\) as a full segment the only way this can happen is when \(\alpha=\beta\).

Order ideals

An order ideal in a poset \((P,\vdash)\) is a subset \(I\) which satisfies the following condition:

For all \(x,y\in P\) if \(x\in I\) and \(x\vdash y\) then \(y\in I\)

Here is another way of describing order ideals. For any \(x\in P\) and \(A\subset P\) we let \[ U(x) := \{ y\in P\ \|\ \ x\vdash y \}\quad\text{and}\quad U(A) := \bigcup_{x\in A} U(x)\ \] Then \(I\subseteq P\) is an order ideal if for every \(x\in I\) we also have \(U(x)\subseteq I\).

Recasting the original problem

I can now recast the original problem: develop an algorithm which constructs \(U(A)\) the order ideal in \((P(G),\vdash)\) which contains a given subset \(A\subseteq P(G)\).

An algorithm

Today’s algorithm will use the algorithms Beginning-At and Ending-At from an earlier post. Respectively, the Beginning-At and Ending-At algorithms construct the set of all paths in \(G\) beginning and ending at a given vertex \(v\in V\). Today’s algorithm in pseudo-code is as follows;

Function Order-Ideal
    Input: a set A of paths
    Output: the order ideal U(A) which contains A
    Initialize: F <- {}
Begin
    For each alpha in A do
        Let a <- source(alpha) and b <- target(alpha)
        For each beta in Beginning-At(b) do
            For each gamma in Ending-At(a) do
                Add the concatenation gamma*alpha*beta to F
            End for
        End for
    End for
    Return F
End function

The lisp code

I will use the following graph to test our code:

(defparameter G '((0 1) (0 2) (1 4) (4 5) (2 5) (5 6) (4 6) (6 7) (3 4) (5 8)))
G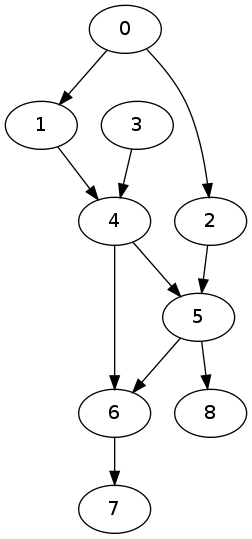

First, I need the code for concatenating paths:

(defun concat (alpha beta)
       (append alpha (cdr beta)))
CONCAT

Now, the code for the main function: I will pass the graph to the function as an argument together with the set of paths as a list.

(defun order-ideal (A G)
    (loop for alpha in A
          append (let ((a (car alpha))
                       (b (car (reverse alpha))))
                      (loop for beta in (beginning-at b G) 
                            append (loop for gamma in (ending-at a G) 
                                         collect (concat gamma (concat alpha beta)))))))
ORDER-IDEAL

And our test

(order-ideal '((2 4 5) (1 3)) G)
((2 4 5) (0 2 4 5) (2 4 5 8) (0 2 4 5 8) (2 4 5 6) (0 2 4 5 6) (2 4 5 6 7)
 (0 2 4 5 6 7) (1 3) (0 1 3) (1 3 4) (0 1 3 4) (1 3 4 6) (0 1 3 4 6)
 (1 3 4 6 7) (0 1 3 4 6 7) (1 3 4 5) (0 1 3 4 5) (1 3 4 5 8) (0 1 3 4 5 8)
 (1 3 4 5 6) (0 1 3 4 5 6) (1 3 4 5 6 7) (0 1 3 4 5 6 7))

I need mention here that the lisp code I wrote for today’s algorithm does not check if the elements in the first argument A are really paths in graph G which is sent as the second argument. For example

(order-ideal '((3 0)) G)
((3 0) (3 0 2) (3 0 2 5) (3 0 2 5 8) (3 0 2 5 6) (3 0 2 5 6 7) (3 0 1)
 (3 0 1 4) (3 0 1 4 6) (3 0 1 4 6 7) (3 0 1 4 5) (3 0 1 4 5 8)
 (3 0 1 4 5 6) (3 0 1 4 5 6 7))

will give us a subset of sequences of vertices which are not really paths in our graph G. So, use the code with caution.