From walks to paths

Description of the problem

Assume \(G = (V,E)\) is an undirected graph. A walk in \(G\) is a sequence of vertices \((v_0,\ldots,v_n)\) such that any two consecutive vertices are connected by an edge. A path, on the other hand, is a walk in which no edges are repeated consecutively. That is \(v_{i-1}\) is not the same as \(v_{i+1}\) whenever the indices make sense.

Today, I will develop an algorithm which returns a path from a given walk by deleting the unnecessary edges.

An algorithm

Let me start with the pseudo-code of the algorithm. I will explain what the algorithm does, and then prove its correctness.

  Function Reduce
     Takes a sequence WALK of vertices as an input
     Returns a sequence PATH of vertices 
  Let PATH and AUX be empty sequences
  While WALK is not an empty sequence do
        If the new first vertex of WALK and the first vertex of PATH agree then
           Discard the first vertices of WALK, PATH and AUX
        Else
           Copy first the vertex of AUX to beginning of PATH
           Move the first vertex of WALK to the beginning of AUX
        End if
  End while
  Return the reverse of PATH

It is easy to see that the time and space complexity of the reduction algorithm are both \(O(n)\) where \(n\) is the length of the walk fed into the algorithm.

The main difference between a path and a walk is that a walk may contain subsequences of the form \(a,b,a\) and we want to remove such subsequences. Imagine our walk is \((a,b,a)\), and we feed it to our algorithm. After the first two runs we get

  WALK = (a)
  PATH = (a)
  AUX = (b)

and in the third run the sequence turns empty as we wanted. Of course the unwanted sequences could be longer. I will handle the general case by induction. Assume our algorithm removes all of the subsequences of the form \((a_1,\ldots,a_{n-1},a_n,a_{n-1},\ldots,a_1)\) which consists of \(n\) edges, and assume we feed a walk which consists of a subsequence \((a_1,\ldots,a_n,a_{n+1},a_n,\ldots,a_1)\) which consists of \(n+1\) edges. When our algorithm hits \(a_1\) at the top of WALK there are three cases:

1. It is possible that the vertex at the top of PATH is the same as \(a_1\) and we discard \(a_1\) together with the vertices at the top of PATH and AUX, and the length of our subsequence reduces by 1. The rest can be handled by the inductive hypothesis.

2. At any stage of the algorithm before we reach \(a_{n+1}\), a reduction might occur in which we have the same vertex appears at the top of WALK and PATH. This means there is a short subsequence of the form \((a,b,a)\) within WALK. Then the algorithm discards elements at the top of the lists WALK, PATH and AUX. Then the state now becomes indistinguishable from processing the sequence WALK in which the subsequence \((a,b,a)\) is replaced by a single vertex \(a\). The rest can be handled by the induction hypothesis.

3. The algorithm might continue without any reduction until we reach \(a_{n+1}\) and it moves at the top of AUX. Then because we reached \(a_{n+1}\) without a reduction, \(a_{n-1}\) appears at the top of PATH and WALK. So, we will have a reduction and we can handle the rest by the induction hypothesis.

An implementation in lisp

For testing purposes I will use the following graph:

(defparameter G '((0 1) (1 2) (1 3) (2 3) (3 4)))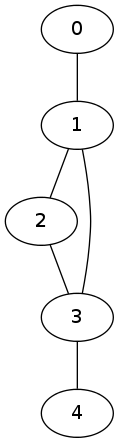

The function is as follows

(defun from-walk-to-path (walk &optional (path nil) (aux nil))
    (cond ((null walk) (reverse (cons (car aux) path)))
          ((null aux) (from-walk-to-path (cdr walk) 
                                         path 
                                         (cons (car walk) aux)))
          (t (let ((a (car walk))
                   (b (car path))
                   (c (car aux)))
                  (if (equal a b) 
                      (from-walk-to-path (cdr walk) 
                                         (cdr path) 
                                         (cdr aux))
                      (from-walk-to-path (cdr walk) 
                                         (cons c path) 
                                         (cons a aux)))))))

Let us test our function on a proper path which requires no reduction:

(from-walk-to-path '(0 1 2 3 4))
(0 1 2 3 4)

Now, I will test it on two walks which require reduction.

(from-walk-to-path '(0 1 2 3 2 1 3 4 3 2 1))
(0 1 3 2 1)

(from-walk-to-path '(0 1 2 3 2 1 3 1 2 3 2 3 1 3 4 3 1 3 4))
(0 1 2 3 4)