Eccentricity, Radius and Diameter in an Undirected Graph

Description of the problem

Given an undirected connected graph \(G = (V,E)\) without loops there is a well-defined notion of distance between two vertices \(x,y\in V\). The distance between \(x\) and \(y\) (which I will denote by \(d(x,y)\) is defined geodesically: it is the length of the shortest path between \(x\) and \(y\).

If the graph comes with weighed edges (i.e. carry numerical values), then instead of calculating the length of a path merely counting the number of edges in a path, we can calculate the total weight of a path by adding the weights of edges appering in that path. In that case, the distance is defined similarly. In fact, we can recover the original notion of the distance if we set the default weight of each edge to 1.

Now, we can define the three notions that I am going to use in this post: the eccentricity of a vertex, the radius and diameter of a graph.

Given a vertex \(x\in V\), the eccentricity of a vertex is the maximum of all distances at \(x\). In other words \[ Ecc(x) := \max \{d(x,y)\|\ y\in V \} \] Now, we can also define the diameter and the radius of a graph as follows: \[ rad(G) := \min \{Ecc(x)\|\ x\in V\} \] \[ diam(G) := \max \{Ecc(x)\|\ x\in V\} \] There is a nice shortcut defining the diameter though \[ diam(G) = \max_{x\in X}Ecc(x) = \max_{x\in X}\max_{y\in X} d(x,y) \] In other words, the diameter is the maximum of all possible distances between all pairs of vertices.

Today, I would like to construct algorithms with functioning lisp code which calculate these quantities for a given undirected graph.

A solution

Eccentricity algorithm

The algorithm for calculating the eccentricity of a vertex \(v\in V\) is going to gradually remove vertices and edges until the graph is empty. The number of steps until the graph becomes empty will give us the eccentricity of that vertex. The pseudo-code is as follows:

function Ecc(x)
  A <- {x}
  n <- 0
  while E is not empty do
     B <- {} 
     for each y in A do
        add neighbors of y to B
        remove all edges adjacent to y
     end for
     A <- B
     n <- n+1
  end while
  return n
end function

The set \(A\) initially contains only the vertex \(x\), and \(B\) is the empty set. Our counter \(n\) is initially \(0\). Now, for each vertex \(y\) in \(A\) we add the vertices connected to \(y\) to the set \(B\) and remove \(y\) together with all edges adjacent to \(y\). Note that it is crucial that \(G\) contains no loops as we do not want a vertex to be nieghboring itself via a loop. At the end of the for each loop \(B\) contains the set of neighboring vertices to the vertices in \(A\) and \(G\) lost all edges adjacent to the vertices in \(A\). We increase the counting index by one.

Complexity and correctness of the eccentricity algorithm

Let me show that the algorithm works correctly. Consider the penultimate step in the algorithm. The set \(A\) will contain vertices which will make the edge set empty when we remove the adjacent vertices. Let \(y\) be one of these vertices in \(A\) at this step. If there were a shorter path from \(x\) to \(y\) of length smaller than the value of the counter \(n\), we would have removed \(y\) earlier and \(y\) would not have appeared in \(A\) in this step. In other words, a vertex is removed at step \(n+1\) (i.e. when the counter is \(n\)) when its distance to \(x\) is \(n+1\). This means the distance between \(x\) and \(y\) is \(n+1\). Hence \(Ecc(x)\geq n+1\). If the eccentricity of \(x\) were strictly greater than \(n+1\) caused by a vertex \(z\in V\) with \(d(x,z)\>n+1\) this vertex could not have been removed earlier because the distance between \(z\) and \(x\) is greater than \(n+1\). If such a vertex exists then there are going to be edges remained after this step which is not possible. So \(Ecc(x)\leq n+1\) too showing that the algorithm works correctly.

The time complexity of the algorithm is \(O(\|V\|\|E\|^2)\).

The distance algorithm and its correctness

We can modify the eccentricity algorithm slightly to get the distance algorithm as follows

function d(x,y)
   A <- {x}
   n <- 0
   while y is not in A
       B <- {}
       for each z in A do
           add neighbors of z to B
           remove all edges adjacent to z
       end for
       n <- n+1
       A <- B
   end while
   return n
end function

I already gave the argument for correctness of this algorithm above when I showed the correctness of the eccentricity algorithm.

Lisp implementation

The data structure

For the lisp implementation, I will assume that each edge is represented by a list of integers of length 2 such as (1 0) where the integers are used as labels for the vertices. I will assume each vertex has a distinct non-negative integer label. For testing purposes, let us define a graph:

(defparameter G '((0 1) (1 2) (1 3) (3 4) (4 5) (2 4) (3 5) (0 6) (2 6)))
G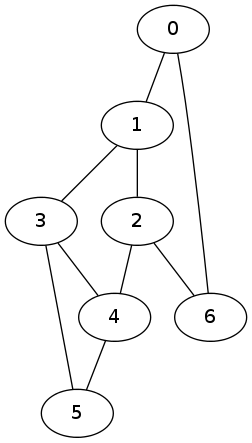

Eccentricity, the radius and the diameter

Now, I will need a function which extracts the set of vertices from a given set of edges

(defun vertices (x) (sort (remove-duplicates (reduce 'append x)) '<))
VERTICES

Let us test it on \(G\)

(vertices G)
(0 1 2 3 4 5 6)

Now, I need a function which lists the neighbors of a vertex \(x\).

(defun neighbors (x G) 
   (let ((H (append G (mapcar 'reverse G)))
         res)
      (dolist (y H) (if (equal (cadr y) x) (push (car y) res)))
      (remove-duplicates res)))
NEIGHBORS

Let us test it on \(G\).

(mapcar (lambda (x) (neighbors x G)) (vertices G))
((6 1) (3 2 0) (6 4 1) (5 4 1) (5 2 3) (3 4) (2 0))

Next, I am going to need a function which removes the edges adjacent to a given vertex

(defun remove-adjacent (x G) 
   (remove-if (lambda (u) (or (equal (car u) x) (equal (cadr u) x))) G))
REMOVE-ADJACENT

and we test if on \(G\).

(remove-adjacent 2 G)
((0 1) (1 3) (3 4) (4 5) (3 5) (0 6))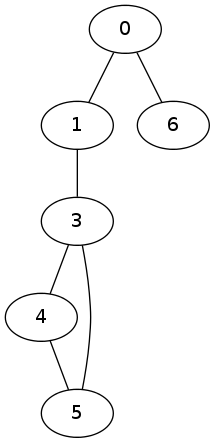

Finally, we are ready to implement the eccentricity and the distance functions.

(defun eccentricity (x G)
   (let ((A (list x))
         (B nil)
         (H G))
      (do ((n 0 (1+ n)))
          ((null H) n)
         (setf B (loop for y in A append (neighbors y H)))
         (dolist (y A) (setf H (remove-adjacent y H)))
         (setf A B))))
ECCENTRICITY

And we test it on \(G\).

(mapcar (lambda (x) (eccentricity x G)) (vertices G))
(4 3 3 3 3 4 4)

That little piece of code is also the basis of our calculation of the radius and the diameter. The function below returns first the radius and then the diameter as a list.

(defun radius-diameter (G)
    (let ((base (mapcar (lambda (x) (eccentricity x G)) (vertices G))))
       (list (reduce 'min base) (reduce 'max base))))
RADIUS-DIAMETER

And we test it on \(G\).

(radius-diameter G)
(3 4)

The distance function

The implementation of the distance function is going to be similar to the implementation of the eccentricity function

(defun distance (x y G)
   (let ((A (list x))
         (B nil)
         (H G))
      (do ((n 0 (1+ n)))
          ((member y A) n)
         (setf B (loop for y in A append (neighbors y H)))
         (dolist (y A) (setf H (remove-adjacent y H)))
         (setf A B))))
DISTANCE

Let us test this on \(G\)

(loop for i from 1 to 12 collect 
   (let ((x (random 6)) (y (random 6))) (list x y (distance x y G))))
((5 1 2) (3 0 2) (1 0 1) (3 1 1) (2 4 1) (4 5 1) (3 3 0) (5 5 0) (1 3 1)
 (4 0 3) (3 0 2) (0 1 1))