Source code entropy
Description of the problem
There is a very beautiful way of calculating the information content of a channel. This measure, called Shannon Entropy, measures the randomness of a signal. And the idea is that the more random the signal is the more information it contains.
Today, I am going to apply this idea to randomly collected source code from various languages.
Calculation
The entropy of a text which uses an alphabet of \(n\) symbols is \[ \sum_{i=1}^n - p_i \log(p_i) \] where \(p_i\) is the probability of seeing \(i\)-th letter in the text, assuming we order our alphabet \(a_1,\ldots,a_n\). Thus if we had all of our letters appearing equally likely, the entropy would have been \[ n\cdot\left(\frac{1}{n}\log(n)\right) = \log(n) \] In our case we consider the letters 33 to 126 in the ASCII table. This is a total of 94 letters giving \(log(94) = 4.543\).
Implementation
For the purposes I set up, I need to calculate the entropy of a given
text. This could be a news article, or source code or a text of a web
page etc. Here is a C program doing exactly that. It reads
an input text from standard input and calculates the entropy and the
number of characters minus the white space.
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main() {
unsigned long table[256], total = 0;
double entropy = 0;
char c;
short i;
for(i=0; i<256; i++)
table[i] = 0;
while((c = getchar())!=EOF)
table[c]++;
for(i=33;i<127;i++)
if(table[i]) {
total += table[i];
entropy -= log(table[i])*table[i];
}
entropy /= total;
entropy += log(total);
printf("Total Characters: %6d\n",total);
printf("Entropy: %5.6f\n",entropy);
exit(0);
}Now, I need some randomly collected source code from various languages. As a reference I am going to calculate the entropy for texts from natural language. For that I used few Jack London books from Project Gutenberg’s website. As for the source code from different languages, it would be best to compare the codes which essentially perform the same task to reduce the variation. For that reason, I used AIMA’s code repository which provide code bases in languages java, C++, lisp, prolog and python.
Here are the results for these languages:
| Source | Size of data | Entropy |
|---|---|---|
| c++ | 407737 | 3.476 |
| java | 1349032 | 3.638 |
| lisp [case sensitive] | 287749 | 3.595 |
| lisp [not case sensitive] | 287749 | 3.397 |
| prolog | 102322 | 3.679 |
| python | 152445 | 3.603 |
| Jack London | 1859084 | 3.127 |
| Totally random [case sensitive] | 4.543 | |
| Totally random [not case sensitive] | 4.220 |
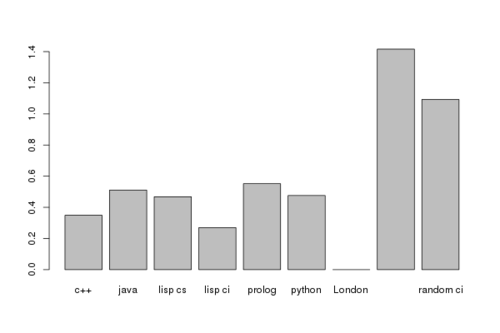
In the graph above, I normalized the numbers by subtracting the Shannon Entropy value for the texts from Jack London.
Interpretation
The natural language text is the least random, thus has the minimal raw information content. I found it surprizing that java and prolog were close and generated the highest values. On the outset, java and prolog are very very different languages. But yet in terms of raw information content of the source code they are close. This interesting. On the other hand python and lisp were in the same class in this comparison if were to treat the lisp code as case sensitive. Once we treat lisp as case insensitive the raw information content drops sharply. However, the drop from case-sensitive to not-case-sensitive in lisp [which is roughly 6%] is similar to the drop in the fully random case [which is roughly 7%]. And in terms of source code raw information content c++ had the smallest value among all case sensitive languages. The case insentive lisp code has the smallest raw information content.
One big shortcoming of the methodology.
I should have removed all comments from the sources to compare the parts of the code that actually do the real work, but I did not.