Transitive closure of a directed graph
Description of the problem
A directed graph \(G=(V,E)\) is called transitive if for every pair of vertices \(a,b\in V\) if there is a path from \(a\) to \(b\) then \((a,b)\in E\). The transitive closure of \(G\) is the smallest transitive subgraph of the complete graph \(K(V) := (V, V\times V)\) containing \(G\).
Today I will look into developing an algorithm which constructs the transitive closure of a directed graph.
A solution
The algorithm works as follows: for every pair of vertices \(a,b\in V\) we will check if there is a path between them. If this is the case, then we will add an edge of the form \((a,b)\) to \(E\).
import igraph
def transitiveClosure(G):
for a in G.vs():
for b in G.vs():
u = a.get_shortest_paths(b)
if len(u[0]) > 2:
G.add_edge(a,b)
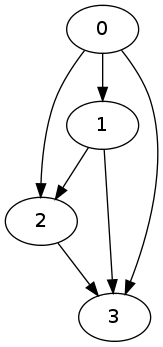
return GConsider the following graph before the closure operator.
g = igraph.Graph(4)
g.to_directed()
g.add_edges([(0,1),(1,2),(0,2),(2,3)])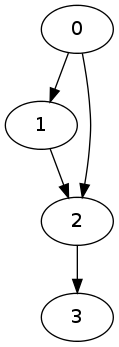
And now, after the closure operator.