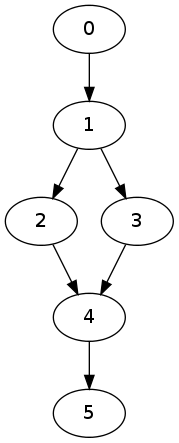
Hasse subgraph of a directed graph
Description of the problem
Let \(G = (V,E)\) be a directed graph. For the purposes of this note, assume that \(G\) has no multiple edges. In other words, assume \(E\) is a subset of \(V\times V\). We would like to understand the connectivity of \(G\) in its minimal form.
A subgraph \(H\) of \(G\) is called a Hasse subgraph if
- \(H\) contains all the vertices of \(G\).
- For any pair of vertices \(a,b\in V\), there is a path connecting \(a\) to \(b\) in \(G\) if and only if there is a path in \(H\) connecting \(a\) to \(b\).
- If \((a,b)\) is a directed edge in \(H\), then every path connecting \(a\) to \(b\) in \(H\) contains the edge \((a,b)\).
Today, I would like to develop an algorithm which constructs a Hasse subgraph of a given directed graph.
A solution
I am going to use igraph
python library to perform basic operations on graphs. Here is an example
of a directed graph defined using the igraph library.
import igraph
g = igraph.Graph(4)
g.to_directed()
g.add_edges([(0,1),(1,2),(0,2),(2,3)])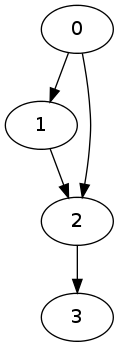
One must give the number of vertices at the time of definition. The
vertices are labelled as \(0,\ldots,n\)
for a graph of size \(n+1\). Also, for
igraph the default is a undirected graph, and one must
declare a graph as directed in our case
The algorithm will remove an existing edge \((a,b)\) first, and then will check if there is a path between \(a\) and \(b\). If there is a path then the edge \((a,b)\) is not needed, and we put \((a,b)\) back in otherwise.
def Hasse(G):
for edge in G.get_edgelist():
G.delete_edges([edge])
paths = G.get_shortest_paths(edge[0],edge[1])
if len(paths[0]) == 0:
G.add_edges(edge)
return GIn the python code above, the igraph library function
get.shortest_paths(a,b) will return the list of shortest
paths from the first vertex a to the second vertex
b. If such a path exists then the edge \((a,b)\) is not needed.
Let us see how this algorithm works in some examples. Consider the following graph
g = igraph.Graph(6)
g.to_directed()
g.add_edges([(2,4),(0,1),(0,2),(0,3),(3,4),(1,3),(1,5),(0,5),(1,2),(0,4),(4,5)])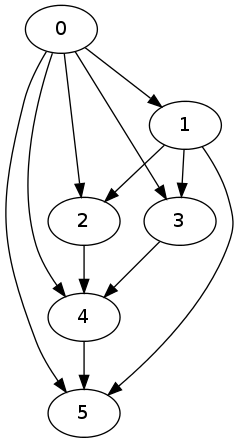
Now, let us see how this graph looks like after we apply our algorithm.